Опр.
Движением называется такое
преобразование плоскости, которое не меняет расстояний: ![]() .
(Опр.: Биективное отображение множества на себя наз-ся проеобразованием этого
множества. Опр.: Отображение называется биективным, если у каждого образа есть
прообраз и при том только один). СВ-ВА:
.
(Опр.: Биективное отображение множества на себя наз-ся проеобразованием этого
множества. Опр.: Отображение называется биективным, если у каждого образа есть
прообраз и при том только один). СВ-ВА: ![]() При
движении окружность
При
движении окружность![]() в окружность того же радиуса.
в окружность того же радиуса.
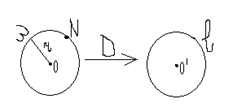 Пусть
Пусть ![]() - произвольная окружность с центром О.
- произвольная окружность с центром О.
Пусть движение принадлежащее к группе движений (![]() ) – произвольное. Обозначим
) – произвольное. Обозначим
![]() . Пусть
дана окружность
. Пусть
дана окружность ![]() . Покажем, что движение D
окружность
. Покажем, что движение D
окружность ![]() . Покажем, что множество
. Покажем, что множество ![]() . Пусть
. Пусть ![]() . 1)
Пусть
. 1)
Пусть ![]() -произвольная, пусть движение D:
-произвольная, пусть движение D:![]() . Т.к. D – движение, то
. Т.к. D – движение, то ![]() . Т.о.
. Т.о. ![]() , значит
любfz точка N принадлежит окружности w:
, значит
любfz точка N принадлежит окружности w: ![]() . 2)Пусть точка
. 2)Пусть точка ![]() (эль-окружность)
– произвольная. Т.к. D – движение, то
(эль-окружность)
– произвольная. Т.к. D – движение, то ![]()
![]() -движение. Пусть
-движение. Пусть 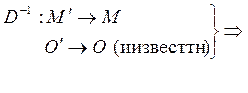
![]()
![]() домножим на D слева
обе части этого равенства:
домножим на D слева
обе части этого равенства: ![]() . Т.о.
. Т.о. ![]() . Из (*) и (**)
. Из (*) и (**)![]() .
Ч.т.д.
.
Ч.т.д. ![]() При движении отрезок
При движении отрезок ![]() в отрезок, луч – в луч, прямая в прямую.
в отрезок, луч – в луч, прямая в прямую. ![]()
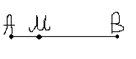
Док-во: Пусть ![]() . Покажем, что
. Покажем, что ![]() ,
,
(![]() -образ отрезка АВ). Пусть точка М лежит
внутри отрезка АВ (
-образ отрезка АВ). Пусть точка М лежит
внутри отрезка АВ (![]() ), и пусть точка М-произвольная.
Пусть движение
), и пусть точка М-произвольная.
Пусть движение ![]() , D – движение,
поэтому
, D – движение,
поэтому ![]() . Т.к. М лежит внутри отрезка АВ (
. Т.к. М лежит внутри отрезка АВ (![]() ), то АМ+МВ=АВ
), то АМ+МВ=АВ![]()
![]()
![]()
![]()
![]()
![]() Пусть
Пусть
![]() , т.е.
, т.е. ![]() . Пусть
. Пусть
![]() , т.к.
, т.к. ![]() -движение,
то АМ+МВ=АВ
-движение,
то АМ+МВ=АВ![]()
![]() . Т.о.
. Т.о. 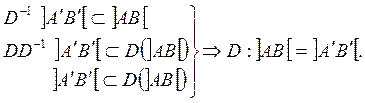
Для луча и прямой док-ва аналогичны.
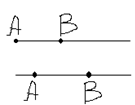
Луч ![]()
Прямая 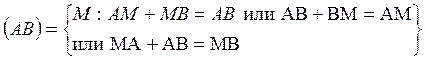
![]() Придвижении пересекающиеся прямые переходят в пересекающиеся прямые, а
параллельные прямые – в параллельные прямые.
Придвижении пересекающиеся прямые переходят в пересекающиеся прямые, а
параллельные прямые – в параллельные прямые.
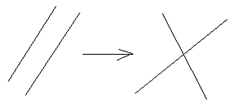 Пусть прямые а и в – параллельные, пусть
движение
Пусть прямые а и в – параллельные, пусть
движение ![]() Док-во методом от противного, прямые
Док-во методом от противного, прямые ![]() не параллельны,
не параллельны, ![]() , тогда
у k два прообраза.
, тогда
у k два прообраза. ![]() При
движении сохраняются углы между прямыми. Дано:
При
движении сохраняются углы между прямыми. Дано: ![]() Т.д.
Т.д. ![]() . Док-во:
. Док-во:
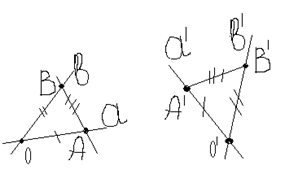 Пусть движение
Пусть движение ![]() . Т.о.
. Т.о.
![]() Ч.т.д.
Ч.т.д.
Т Теорема: Множество всех движений плоскости образует
Группу.
Док-во: 1. Покажем, что для любых движений ![]() принадлежащих
группе движений, композиция
принадлежащих
группе движений, композиция ![]() . Пусть А,В –
произвольные точки плоскости.
. Пусть А,В –
произвольные точки плоскости.
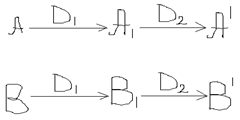
Т.е. ![]()
Т.к. 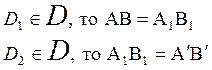
![]()
![]() -движение.
-движение.
2.
Пусть движение D из
группы движений – произвольное(![]() ), покажем, что
), покажем, что ![]() -движение. Пусть
-движение. Пусть ![]() -
произвольные точки. Пусть движение
-
произвольные точки. Пусть движение ![]() . Т.к. D –
движение, то
. Т.к. D –
движение, то ![]() .Ч.т.д.
.Ч.т.д.
Теорема
о задании движения: Каковы бы ни были
два равных треугольника ![]() , существует
единственное движение, переводящее
, существует
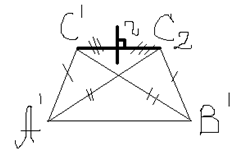
единственное движение, переводящее ![]() . Док-во: Существование.
Рассм. осевую симметрию, переводящую
. Док-во: Существование.
Рассм. осевую симметрию, переводящую ![]() : (
: (![]() p – серединный перпендикуляр
p – серединный перпендикуляр ![]() ), при этом
), при этом ![]() . q –
серединный перпендикуляр
. q –
серединный перпендикуляр ![]() , т.к.
, т.к. ![]() , то
, то ![]() .
.
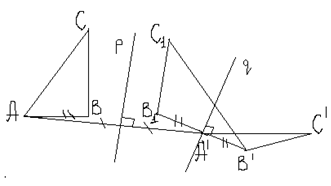
![]() .
.
Получится:
r – серединный перпенд-р ![]()
Докажем
единственность: От противного, движение ![]() ,
, ![]() ,
, ![]() . Но при
этом существует такая (•) М, что
. Но при
этом существует такая (•) М, что ![]()
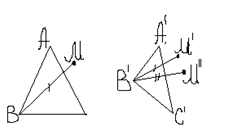 Т.к.
Т.к. ![]() - движения, то
- движения, то ![]()
![]() лежит
лежит
на серединном перпендикуляре отрезка ![]() . Аналогично точки
. Аналогично точки ![]() лежат
на серединном перпендикуляре отрезка
лежат
на серединном перпендикуляре отрезка
![]() ; получаем ?! с тем, что
; получаем ?! с тем, что ![]() - треугольник. Ч.т.д.
- треугольник. Ч.т.д.
Теорема Шаля: Всякое движение первого рода есть либо перенос, либо поворот; всякое движение второго рода есть либо скользящая, либо осевая симметрия.
Определения: Осевой
симм-ей относ-нопрямой р
наз-ся преобразование плоскости, оставляющее (•)-и прямой р неподвижными, а
произвольной (•)-е ![]() ставящей в соответствие такую
(•)
ставящей в соответствие такую
(•)![]() , что р – серединный
, что р – серединный ![]() отрезка
отрезка ![]() .Центр-ой
сим-ей с центром О наз-ся преобразование пл-сти, оставляющее (•) О
на месте, а любой другой (•)-е А, ставящее в соответствие такую (•)
.Центр-ой
сим-ей с центром О наз-ся преобразование пл-сти, оставляющее (•) О
на месте, а любой другой (•)-е А, ставящее в соответствие такую (•)![]() , что О – середина отрезка
, что О – середина отрезка![]() . Парал-ным переносом на вектор
. Парал-ным переносом на вектор ![]() наз-ся преобразование пл-сти, ставящее в
соответствие произвольной (•) А такую (•)-у
наз-ся преобразование пл-сти, ставящее в
соответствие произвольной (•) А такую (•)-у ![]() Поворотом
на ориентированный угол
Поворотом
на ориентированный угол ![]() относительно (•) О
наз-ся преобр-ние пл-сти, ставящее в соответствие произвольной (•) А такую (•)
относительно (•) О
наз-ся преобр-ние пл-сти, ставящее в соответствие произвольной (•) А такую (•)![]() , что выполняются два условия:
, что выполняются два условия: ![]() Скользящей симм-ей наз-ся композиция
осевой симм-ии и I I-ного переноса на ненулевой вектор
I I-ный оси симметрии.
Скользящей симм-ей наз-ся композиция
осевой симм-ии и I I-ного переноса на ненулевой вектор
I I-ный оси симметрии.
С движением уч/ся знакомятся в конце 9 кл.: дается понятие отображения плоскости на себя, осевая симметрия, понятие движения, движения плоскости, центральной симметрий, параллельный перенос, поворот.
В 11 кл., изучается в теме «метод координат в пространстве». Дается понятие центр, осевая, зеркальная симметрия и параллельный перенос. На базовом уровне эта тема практически не изучается.В классах с УИМ тема «Движение» может быть также изучена в главе «М-д корд-т». На изучение темы следует отвести 6-10 ч. При изучении преобразования в геом-ии не рассм-ся пр-сс во времени, а ограничиваются сопоставлением исходной фигуры и фигуры, полученной в рез-те преобразования. Уч-ся уже встречались с отображением фигур на фигуру, знакомы с понятием «преобразование пл-сти», т.е. отображение пл-сти на себя.
Задача: Пусть движение f:![]() . Выяснить явл-ся ли D: а) обратимым,
б) имеет ли неподвижные (•)-и. Реш-ие: а) f:
. Выяснить явл-ся ли D: а) обратимым,
б) имеет ли неподвижные (•)-и. Реш-ие: а) f: ![]() ,
, ![]() ,
, ![]() движение обратимо. б) О(0,0,0) –
неподвижная (•)-а.
движение обратимо. б) О(0,0,0) –
неподвижная (•)-а.
Эстетика – наука о чувственном познании, создающем прекрасное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.