Решение системы линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса

Привести систему к системе с базисом методом Жордана Гаусса и найти одно базисное решение.

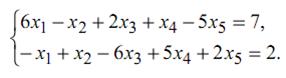
Заполним таблицу Гаусса. Будем также преобразовывать разрешающие элементы в единицу. Из элементарных преобразований следует, для этого нужно каждую разрешающую строку делить на соответствующий разрешающий элемент.

6	-1	2	1	-5	7
-1	1	-6	5	2	2
5	0	-4	6	-3	9
-1	1	-6	5	2	2
1	0	-4/5	6/5	-3/5	9/5
0	1	-6	6	7/5	3

в результате двух итераций система преобразовалась к трапециидальному виду.

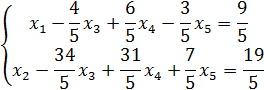
Следовательно, исходная система имеет бесчисленное множество решений.

Последняя система очевидным образом разрешается относительно базисных неизвестных ,  (– свободная неизвестная):

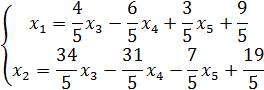
Базисным решением системы называется всякое ее решение, в котором свободные пе- ременные равны нулю.

тогда

- базисное решение

Задание 6. Найти два опорных решения канонической системы уравнений.

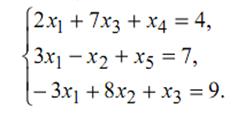
Матрица А и расширенная матрица Ā данной системы имеют одним из миноров высшего порядка минор второго порядка

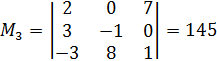
который отличен от нуля. Следовательно, r(А) = r(Ā) = 3. Система совместна, и так как

r < n (n = 5), то она имеет бесчисленное множество решений. Число ее базисных решений не превосходит числа . Некоторые группы из двух переменных будут базисными. Так как n – r = 5 – 3 = 2, то свободными будут три переменные.

Базисные решения будем находить путем перебора возможных базисных переменных и решения соответствующих систем уравнений со свободными переменными, равными нулю.

Так как минор

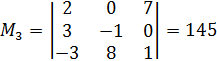
при неизвестных  отличен от нуля, то этот минор является базисным (ранговым), а неизвестные  – базисными (тогда – свободные неизвестные). Полагаем в системе  . Получим следующую систему уравнений для нахождения неизвестных  :

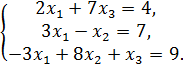
Решим систему , используя формулы Крамера:

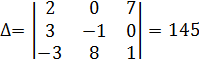
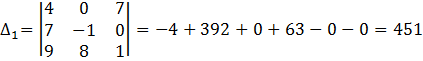
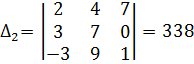
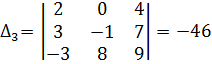
Таким образом, первое базисное решение есть . Оно же является и опорным решением.

Рассмотрим минор при неизвестных :

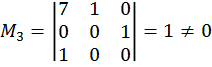
Неизвестные  являются базисными, а  – свободными. Полагая  , приходим к системе уравнений

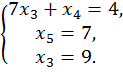
которая имеет следующее решение: . Имеем второе базисное решение , которое так же является опорным.

Задание 7. Найти собственные значения и собственные векторы данной матрицы.

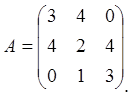
Характеристическое уравнение этой матрицы имеет вид

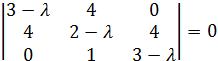
или

Его характеристические корни  являются собственными числами.

Собственный вектор, соответствующий собственному значению , находится из системы уравнений, которая для данной ситуации имеет вид

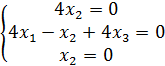
её решением является вектор  с произвольным действительным числом с. Тогда каждый вектор , где с ≠ 0, является собственным вектором с собственным значением .

Собственный вектор, соответствующий собственному значению , находится из системы уравнений, которая для данной ситуации имеет вид

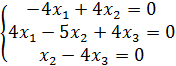
Решим систему методом Гаусса:

-4	4	0	0
4	-5	4	0
0	1	-4	0
-4	4	0	0	:-4
0	-1	4	0
0	1	-4	0
1	-1	0	0
0	-1	4	0
0	1	-4	0
1	0	-4	0	ранг матрицы равен 2. Последнюю строку вычеркиваем
0	-1	4	0
0	0	0	0
1	0	-4	0
0	1	-4	0

Получили систему

 свободная неизвестная.

Решением системы является вектор  с произвольным действительным числом с. Тогда каждый вектор , где с ≠ 0, является собственным вектором с собственным значением .

Собственный вектор, соответствующий собственному значению , находится из системы уравнений, которая для данной ситуации имеет вид

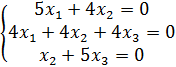
Решим систему методом Гаусса:

5	4	0	0	:4
4	4	4	0
0	1	5	0
5	4	0	0
1	1	1	0
0	1	5	0
0	-1	-5	0
1	1	1	0
0	1	5	0
0	0	0	0	вычеркнем нулевую строку
1	0	-4	0
0	1	5	0
1	0	-4	0
0	1	5	0

Получили систему

 свободная неизвестная.

Решением системы является вектор  с произвольным действительным числом с. Тогда каждый вектор , где с ≠ 0, является собственным вектором с собственным значением .

Задание 8. Даны вершины треугольника АВС. Найти уравнения его сторон и точку пересечения  высот.

Запишем уравнения сторон треугольника используя формулу

АВ:                                                                

BC:

AC:

Высоты треугольника пересекаются в одной точке, значит достаточно найти уравнения двух высот и найти точку их пересечения.

Запишем уравнение высоты из точки А. Данная высота перпендикулярна прямой ВС. Прямая ВС приводится к виду :

Так как , то согласно условию перпендикулярности прямых, угловой коэффициент перпендикулярной прямой  .Воспользовавшись уравнением , получим ,

Запишем уравнение высоты из точки C. Данная высота перпендикулярна прямой AB. Прямая AB приводится к виду :

Так как , то согласно условию перпендикулярности прямых, угловой коэффициент перпендикулярной прямой  .Воспользовавшись уравнением , получим ,

Для того, чтобы найти точку пересечения, решим систему уравнений