4.2.Уточнённая модель
Полное аналитическое описание частотной характеристики ООВ связано с операциями над трансцендентными уравнениями и приводит к выражениям, сложность которых затрудняет непосредственный анализ их использования для последующих действий с характеристикой.
Полная дисперсия ООВ, как было сказано ранее, состоит из материальной и волноводной составляющих, которые могут быть непосредственно измерены.
Материальная дисперсия:
dtg=-(l/c)l[d2n(l)/dl2]dl ; (4.2.1)
волноводная дисперсия:
dtl=-(l/c)w[d2b(w)/dw2]dw , (4.2.2)
где l – длина волокна, c – скорость света, n(l) – зависимость показателя преломления от длины волны l, а b(w) - зависимость постоянной распространения от частоты w.
На основании (4.2.1) получаем:
dtg=-(l/c)w[d2n/dw2]dw ; (4.2.3)
где dw - ширина спектра излучения лазера или спектра модуляции (выбирается наибольшее значение). Затухание ООВ для всей области частот, вплоть до частоты отсечки второй моды, может быть принятым постоянным (a=const), поэтому в пределах одномодового режима модуль ЧХ |KE(w)|=1, и следовательно, частотная характеристика
KE(jw)=ejb(w)×l . (4.2.4)
Воспользуемся следующими исходными выражениями применительно к основной моде ООВ со ступенчатым профилем n(r):
b=(1/a)[(n2/2D)-u2]1/2, (4.2.5)
где a – радиус сердцевины ООВ, u=g1a; g1,g2 – поперечные волновые числа для сердцевины и оболочки соответственно;
n2=u2 + w2; w=g2×a; g12=k12 - b2; g22=b2 - k22, k1,k2 – волновые числа сердцевины и оболочки соответственно; k1,2=(2p/l)n1,2.
Параметры u и w связаны друг с другом трансцендентным характеристическим уравнением, которое применительно к ООВ и с учётом того, что D=(n1 - n2)/n1<<1, имеет вид
u[J1(u)/J0(a)]=w[K1(w)/K0(w)], (4.2.6.)
где J0,1(u) и K0,1(u) – функция Бесселя и модифицированная функция Ханкеля первого рода.
Характеристическая частота может быть выражена:
![]()
Совокупность уравнений (4.2.5) и (4.2.6) не даёт возможности получить выражение для b(w) в явном виде. Поэтому предварительно найдём ряд численных решений уравнения (4.2.6) относительно u, т.е. найдём числовую зависимость u=f(n) для интервала n=(1,05…2,4). Далее по найденным данным находим аппроксимацию данной функции.
Выбираем функцию такого вида: u=Qnm. Постоянные Q и m подлежат определению. Процесс аппроксимации производим по методу наименьших квадратов, при котором сумма квадратов разности между значениями величин, вычисленных по приведённым выше формулам, и аппроксимирующей функции должна быть минимальна.
Для функции вида u=Qnm значение постоянных могут быть получены из решения двух уравнений:
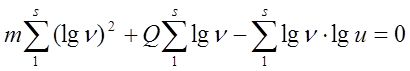 ,
,
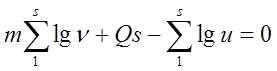 ,
,
где s – количество выборок значений n. В нашем случае s=28. Результаты расчётов, проведённые на ЭВМ, дают: Q=1,08; m=1/2; таким образом,
u=1,08n1/2 (4.2.7)
Ошибка вычислений по формуле (4.2.7) по сравнению со значениями, полученными по формуле (4.2.6) порядка ±(1…2)%. Следовательно,
b=1/2[(n2/2D)-1,17n2]1/2 . (4.2.8)
Оценим порядок слагаемых, входящих в это выражение. Пределы реальной области режима работы и параметров ООВ следующие: n=2…2,4; 0,001£D£0,01.
Примем n=2, D=0,005. Тогда n2/2D=400; 1,170n=2,34. Следовательно,
n2/2D>>1,17n . (4.2.9)
Поэтому в первом приближении, применительно к предварительным оценкам, можно пользоваться простым выражением
b=(1/a)[(n2/2D)-2,34]1/2 . (4.2.10)
В дальнейшем, однако, будем пользоваться формулой (4.2.8).
Полученные выражения относятся к идеализированному ступенчатому профилю n(r). Он используется при решении ряда задач, связанных с распространением сигналов по одномодовому оптоволокну. Реальный профиль несколько отличается от указанного вследствии особенности ряда процессов, происходящих при получении заготовок и вытяжки из них волокна. Основное отличие – отсутствие чёткой границы между сердцевиной и оболочкой. Точное описание реального профиля ООВ (который не является ступенчатым) – затруднительно.
Согласно [5] в общем случае сглаженный профиль описывается выражением:
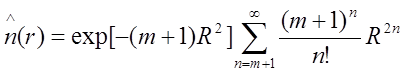 (4.2.11)
(4.2.11)
где R=r/a, r – текущий радиус. В частности при m=0 имеем гауссовый профиль. Анализ (4.2.11) показывает, что при m=(8..10) профиль n(r) близок к реальному «ступенчатому», т.е. сглаженному.
Параметр u для волокна, профиль которого описывается выражением (4.2.11), будет
u=[(m+2)n(2/(m+2)) - (m+1)]1/2 .
При указанных выше значениях m=8 и m=10 и при n=2 соответственно имеем: u=1,57 и u=1,11.
Из изложенного следует, что в случае сглаженного профиля выражение для b(w) отличается только видом второго члена, стоящего в квадратных скобках (4.2.8). Так как средние значения этого слагаемого (1,11…1,57)<2,34 (4.2.10), применительно к сглаженному профилю среднее значение второго члена можно принять равным (1,1…1,6) или. В первом приближении, вообще его опустить, ибо среднее значение первого слагаемого приблизительно равно 400.
Поскольку второе слагаемое определяет влияние волноводной дисперсии, сглаженный профиль снижает последнюю; это следует также из известных физических представлений.
Учтём материальную дисперсию. Обратимся к параметру D(w)=[n1(w) – n2(w)]/n1(w). Так как n1/n2»1, можно с достаточной точностью принять n1(w) – n2(w)=const=dn. Следовательно,
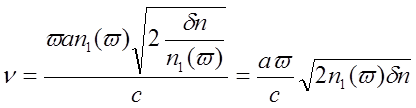
В реальных ООВ величина n1(w) изменяется в пределах n0(1±0,02), где n0 = n1(w0) – исходное значение n1 на несущей частоте w0. Поэтому величина ![]() при изменении w остаётся в пределах q=q0(1±0,01), где
при изменении w остаётся в пределах q=q0(1±0,01), где ![]() . С учётом соотношения (4.2.9) можно
с достаточной точностью принять
. С учётом соотношения (4.2.9) можно
с достаточной точностью принять
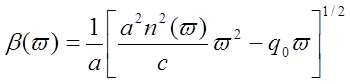
Отсюда следует, что при q0=0 b(w)=[n1(w)/c]w, т.е. нелинейность b(w), а значит искажения сигнала, в рамках принятых приближений, определяются только материальной дисперсией. Член q0w определяет вклад волновой дисперсии.
Полное выражение для b(w), в котором учитывается зависимость q0 от w, имеет вид:
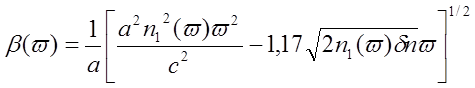
Обозначим n12(w)=y(w) и разложим в ряд, ограничиваясь третьим членом:
y(w)=y(w0)+(w - w0)y’(w0) + [(w - w0)2/2!]y’’(w0).
n12(w)=n02 + 2n0(w – w0)n1’(w0) + (w – w0)2n0n1’’(w).
Выразим n’’(w0); n’(w0) через dtg. На основании (4.2.3), учитывая, что b(w) по смыслу определяется на единицу длины (l=1), находим
n’’(w)=-[dtgc/wdw].
Тогда
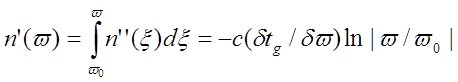 ,
,
но |w/w0|max=|(w0±dw)/w0|»1. Следовательно, n’(w)»0. Отсюда
n2(w)»n02 + n0(dtgc/w0dw)(w – w0)2.
Так как
wmax=w0 + dw и (w - w0)2/w0»2(w - w0),
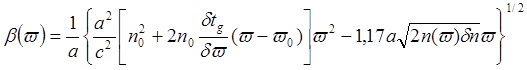 (4.2.12)
(4.2.12)
Поскольку 0 £ w – w0 £ dw, второй член, стоящий в квадратных скобках, изменяется в пределах:
0 £ 2n0(dtgc/dw)(w – w0) £ 2n0dtgc.
Обозначим
2n0(dtgc/dw)(w – w0)=f(w).
Выражение (4.2.12) описывает фазовую характеристику ООВ со ступенчатым профилем n(r), с учётом волноводной и материальной дисперсий. Материальная дисперсия входит в это выражение в явном виде, а влияние волноводной обуславливается нелинейностью выражения [независимо от нелинейности n(w)]. Таким образом, аналитическая связь двух видов дисперсии с общей дисперсией оказывается достаточно сложной.
В случае отсутствия материальной дисперсии имеем
![]()
или, так как n0=n1 и (n1 – n2)/n1=dn/n1=D,
![]()
Нелинейность этого выражения, обусловливающая волноводную дисперсию, определяется наличием второго члена, стоящего в круглых скобках; при его отсутствии b(w)=(w/c)n0, т.е. приходим к выражению для волнового коэффициента линейной среды.
Если преобладает материальная дисперсия, то
b(w)=[n02+2n0(dtg/dw)(w – w0)]1/2.
Из
(4.2.12), обозначив 2n0(dtg/dw)c=A и принимая ww0»w02, а также учитывая, что ![]() , находим первую производную:
, находим первую производную:
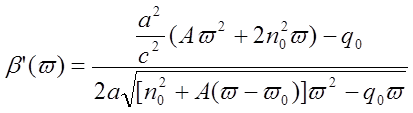 .
.
Максимальное значение полной дисперсии (на границе полосы частот dw) на единицу длины волокна
dt0=vгр-1(w0) – vгр-1(w0+dw)=b’(w) – b’(w0+dw),
где vгр(w) - групповая скорость. На основании (4..2.13) получаем
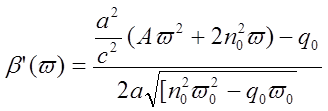 ;
;
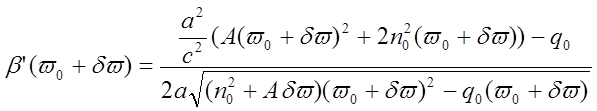 ;
;
Из изложенного следует, в частности, что материальная и волноводная дисперсии образуют полную дисперсию сложным образом и простое или квадратичное их суммирование не даёт значения полной дисперсии, т.е. dt0¹dtg+dtl или dt02¹dtg2+dtl2.
Полная дисперсия dt0 может быть равна нулю, если b’’(w). Однако это реализуется только на одной частоте w’. При этом параметры волокна должны быть выбраны в разумных пределах.
Реальным является не обеспечение dt0=0 на одной частоте w’, а реализация dt0= dt0min, где dt0min - не более некоторого допустимого предела на всём частотном интервале dw (при заданном w0). Для этого достаточно задать в выражении (4.2.14) dt0= dtmin и определить необходимые параметры ООВ.
При отсутствии материальной дисперсии, т.е. при преобладании волноводной, имеем
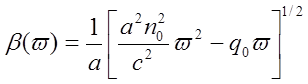 ,
,
откуда
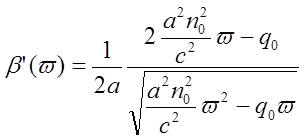 .
.
Волноводная дисперсия
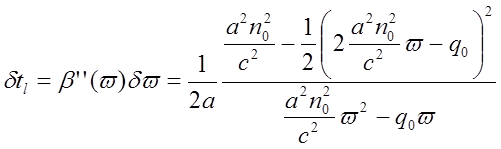 .
.
Из предыдующего следует, что ЧХ одномодового волокна длиной l
K(w;l)=ejb(w)l=K1(w;l)+K2(w;l).
Учитывая, что среднее из возможных значений q0w=2,34 и что 2,34/w<<1, примем
![]() .
.
Переходная характеристика по огибающей:
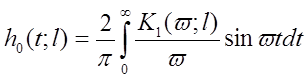 ,
,
Так как K1(w;l)=cos[b(w)l],
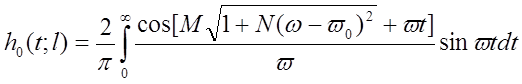 ,
,
где M=(n0/c)l; N=A/n02.
Импульсная характеристика волокна
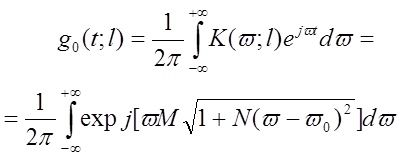
или
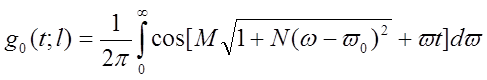 .
.
На основании полученной импульсной характеристики, вычислением свёртки производим расчёт выходного импульса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.