4. Создание математической модели.
4.1. Приближенная модель уширения оптического импульса при распространении по одномодовому оптоволокну.
Как известно, искажения сигналов в одномодовых оптических волокнах (ООВ) возникают из-за:
а) нелинейности характеристики коэффициента распространения (внутримодовая дисперсия);
б) дисперсии в материале волокна, которая является следствием нелинейности показателя преломления n(w) - в зависимости от частоты w.
Влияние эллиптичности поперечного сечения, приводящее к появлению двух поляризованных мод, не учитываем, так как полагаем эту ситуацию дефектной.
Учёт влияния указанных факторов на форму выходного сигнала приводит к сложным выражениям и требует знания функции n(w) или её производных, которые не всегда известны с нужной для расчётов точностью.
Применительно к цифровым системам передачи (ЦСП) нет необходимости в очень точном описании выходного сигнала; достаточно такого, при котором можно определить все требуемые его параметры. Это обстоятельство подтверждается тем, что независимо от ширины полосы принят и рекомендован МККТТ [2] обобщённый параметр, характеризующий свойства ООВ, а именно – полная дисперсия |t| (в пс/км×нм), т.е. временная задержка на единицу полосы спектра излучения лазера Dls (нм), отнесённая к длине волокна L.
Дисперсия является полной потому, что она содержит все составляющие (внутримодовую и материальную). Величина t может быть измерена и таким образом определена дисперсия для конкретных условий:
t0=t×L×Dls .
Отсюда следует, что принята линейная зависимость t0 от L и Dls. В действительности эта связь нелинейна, и в этом заключается допущение, приводящее к приближенным выводам. Так как параметр t задаётся или измеряется непосредственно для каждого волокна, нелинейность зависимости t от n(w) не имеет значения для дальнейших выводов.
По смыслу параметр t должен определяться для единичного импульса 1(t), так как только в этом случае величина t однозначна, а граница интервала запаздывания имеет не асимптотическое, а конечное значение. Итак, рассматриваемая система принимается линейной с одним звеном запаздывания, так как задаётся единственный параметр t0, содержащий длину волокна L. Процессы в такой системе описываются уравнением
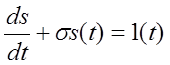 ,
,
решение которого:
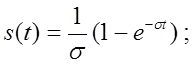
опуская постоянный множитель, получаем переходную функцию h(t). Величина s-1, как известно, постоянная времени системы. При t=s-1h(t)=0,632<1, т.е. процесс не заканчивается и s-1 не является полной задержкой сигнала. Применительно к ООВ величина t0 относится к практически установившемуся сигналу (т.е. к конечному значению запаздывания), поэтому t0>s-1. Обозначим s-1=t0. По существу мы перешли к схеме замещения линии с распределёнными постоянными приближенной системой – к одному звену задержки. В нашем случае такая замена физически правомочна.
Как известно, неадекватность систем с распределёнными и сосредоточенными постоянными выражается в невозможности одновременной тождественности всех характеристик. Однако при рассмотрении одного какого-либо частного параметра (представленного в нашем случае одним элементом задержки) такая замена допускается, а анализ переходных процессов существенно упрощается, причём погрешность такого приближения практически несущественна и целиком определяется единственным исходным критерием, принятым для оценки искажения сигнала, а именно временной дисперсией ООВ.
Найдём постоянную времени ООВ. Примем, что процесс установления h(t) соответствует запаздыванию t0 и практически заканчивается, когда h(t)=0,95. Этому соответствует t/t0»3,0, откуда:
![]() .
.
Таким образом, переходная характеристика ООВ при принятом приближении описывается выражением
![]() ,
,
где s=3/t×Dls×L. Тогда импульсная характеристика ООВ будет иметь вид
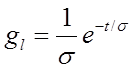 .
.
Зная gl(t), при известном сигнале на входе в волокно, выходной сигнал находим пользуясь интегралом свёртки:
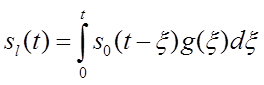
Не сложно найти выражения описывающие выходной сигнал для нескольких типов входных сигналов, но при использовании для вычислений ЭВМ, и для независимости модели от входного сигнала более уместно вычисление интеграла свёртки численными методами. Наиболее быстрое вычисление этого интеграла, при наименьших вычислительных затратах, достигается при применении метода кусочно-параболического циклического суммирования (метод Симпсона) [17].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.