3. The problem is to solve optimal control problem by economy
optimality for the process ![]() for minimum of
expences
for minimum of
expences  when the initial conditions are:
when the initial conditions are: ![]() ,
, ![]() .
.
Solution
1)
First of all we must write phase coordinates: 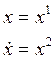
So, this process can be described by the system of differential equations:
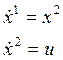
where ![]() - control
parameter.
- control
parameter.
2) Write Hamilton-Pontryagin function for our case:
![]() ,
,
where ![]() - auxiliary functions.
- auxiliary functions.
For finding of control parameter ![]() let’s use the maximal principal, which states that in optimal
process Hamilton-Pontryagin function
let’s use the maximal principal, which states that in optimal
process Hamilton-Pontryagin function ![]() gets maximum value, for existing of which the requirement is
following:
gets maximum value, for existing of which the requirement is
following:
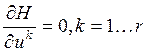
So, we have for our case:
![]()
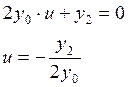
For finding of auxiliary functions ![]() let’s use Hamilton-Pontryagin equation in general form are the
following:
let’s use Hamilton-Pontryagin equation in general form are the
following:
![]()
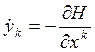
Let’s write it for our case:
![]()
![]()
![]()
![]()

Substituting the got values of auxiliary functions ![]() in formula for finding of
control parameter
in formula for finding of
control parameter ![]() we
obtain:
we
obtain:
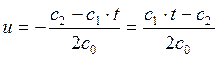 ,
,
Let’s denote our constant in more compact view
![]()
where, 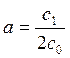 ,
, 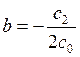 .
.
3)
Let’s return to initial coordinates and synthesize
the phase trajectory ![]() .
.
![]() , so we have
, so we have ![]()
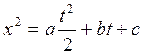
![]()
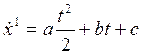
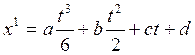
4)
Let’s use the initial conditions: ![]() and
and ![]()
Because of ![]() ,
, ![]() we will have
we will have
 , that’s why we eliminate one constant, it
will be equal to
, that’s why we eliminate one constant, it
will be equal to ![]() .
.
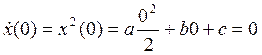 , thus we eliminate the second constant
, thus we eliminate the second constant ![]() .
.
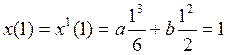
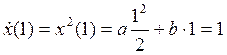
From the system of two last equations we found the rest of constants
![]()
![]()
5) So, we have the control parameter
![]()
and the equation of phase trajectory (fig. 3.1):
![]()
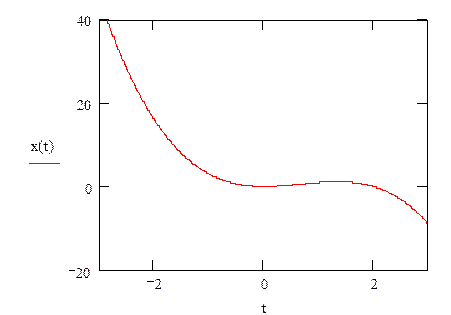
Fig. 3.1 Phase trajectory
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.