The problem is to solve optimal control problem by economy optimality for the process

3. The problem is to solve optimal control problem by economy optimality for the process    for minimum of expences 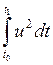 when the initial conditions are: , .

Solution

1)  First of all we must write phase coordinates: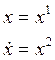

So, this process can be described by the system of differential equations:

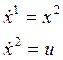
where  - control parameter.

2)  Write Hamilton-Pontryagin function for our case:

,

where  - auxiliary functions.

For finding of control parameter  let’s use the maximal principal, which states that in optimal process Hamilton-Pontryagin function  gets maximum value, for existing of which the requirement is following:

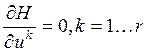
So, we have for our case:

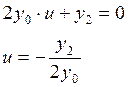
For finding of auxiliary functions  let’s use Hamilton-Pontryagin equation in general form are the following:

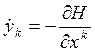
Let’s write it for our case:

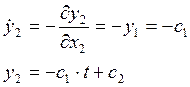
Substituting the got values of auxiliary functions  in formula for finding of control parameter  we obtain:

,

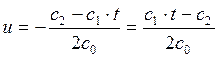Let’s denote our constant in more compact view

where,   , .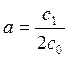

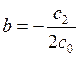3)  Let’s return to initial coordinates and synthesize the phase trajectory .

, so we have

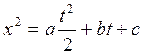
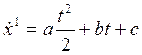
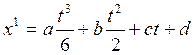
4)  Let’s use the initial conditions:  and

Because of ,   we will have

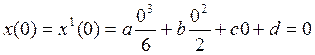, that’s why we eliminate one constant, it will be equal to .

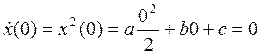, thus we eliminate the second constant .

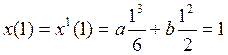
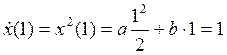
From the system of two last equations we found the rest of constants

5)  So, we have the control parameter

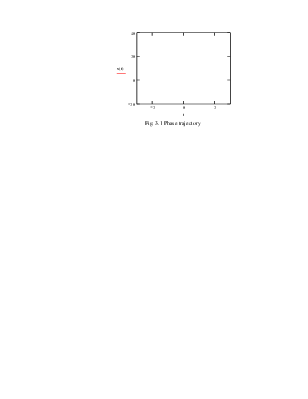
and the equation of phase trajectory (fig. 3.1):

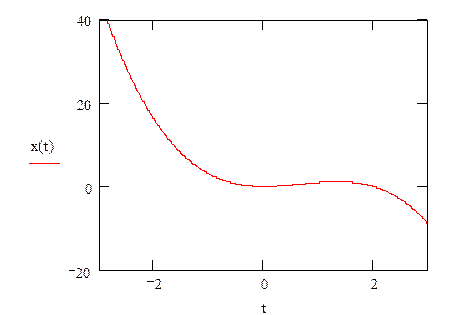
Fig. 3.1 Phase trajectory