Космические ракетные комплексы, страница 2

На рис. 18-1 представлены силы, действующие на РН и соответствующая этим силам диаграмма в связанной системе координат. Необходимо заметить, что вес РН, W, сконцентрирован в центре масс, cg, а аэродинамические силы – подъемная L, и сила сопротивления D, сконцентрированы в центре давления cp. Конфигурация при которой центр масс располагается впереди центра давления является устойчивой, поскольку подъемная сила и сила сопротивления создают восстанавливающий момент относительно центра масс РН. В идеальном случае, сила тяги, Т, направлена по оси симметрии РН, однако, существует возможность создания управляющего момента путем отклонения сопла двигателя. Угол тангажа, f, измеряется от местного горизонта до вектора скорости РН, а угол атаки, a - от вектора скорости до продольной оси РН.

Рис. 18.1.Силы, действующие на РН.

Используя диаграмму, представленную на рис. 18-1 (б) мы можем получить уравнения для определения ускорений относительно продольной a_x и поперечной a_z осей связанной системы координат.

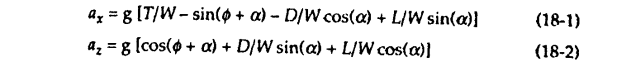
Уравнения (18-1) и (18-2) используются для оценки ускорения РН, представленного в таблице 18-8. Тяга и сопротивление могут рассчитываться с использованием уравнений (17-1) и (6-21), соответственно, Интегрирование уравнений (18-1) и (18-2) в инерциальной системе координат позволяет оценить скорость РН.

Скорость, которую должна обеспечить РН может быть оценена следующим образом:

DV_необх = DV_орб + DV_грав + DV_сопр                (18-3)

где DV_орб - скорость, требуемая для выведения на заданную орбиту. Потери скорости DV_грав и DV_сопр добавляются к идеальной скорости для получения требуемой скорости для выведения на орбиту. Разработчик РН также должен принять во внимание потери скорости за счет системы управления вектором тяги для обеспечения заданной формы траектории и других переменных, таких как температура РДТТ, приводящих к изменению уровня тяги. Типовые значения потерь на гравитацию и сопротивление для двухступенчатой РН представлены на рис. 18-2. Необходимо заметить, что потери на гравитацию и сопротивление атмосферы чувствительны к начальному соотношению тяги к весу, T/W₀. Малое значение соотношения (тяговооруженности) приводит к увеличению потерь на гравитацию, поскольку РН движется в гравитационном поле на большем промежутке времени, в то время, как большая тяговооруженность приводит к увеличению потерь на сопротивление атмосферы. Тяговооруженность является ключевым параметром, поскольку определяет вибрационные, акустические и динамические нагрузки на КА. Эти условия внешней среды и нагрузки обсуждаются в разделе 18.3.

При отсутствии атмосферы и топографических изменений оптимальной траекторией была бы траектория близкая к Гомановскому переходу и потери на гравитацию были бы минимизированы путем создания тяги в направлении перпендикулярном радиус-вектору. Для точной оценки потерь на гравитацию необходимо знать точную траекторию и время полета РН. Для средних и тяжелых РН потери на гравитацию составляют около 750 – 1500 м/с.

Силы аэродинамического сопротивления, действующие на РН, зависят от формы и размеров РН, скорости движения, угла атаки a. Уравнение (6-21) может быть приведено к виду:

D/W = C_d(A/W)q                   (18-4)

где С_d – безразмерный коэффициент сопротивления (около 2,2), А – поперечное сечение РН перпендикулярное вектору скорости РН, q - скоростной напор, действующий на РН. Скоростной напор равен половине произведения плотности атмосферы на квадрат скорости. Для существующих на сегодняшний день тяжелых РН потери скорости за счет сопротивления атмосферы не превышают 3% от общей требуемой скорости, что составляет приблизительно от 20 до 40 м/с. Доля затрат на сопротивление атмосферы падает с уменьшением размера РН.

Рис. 18-2.Потери энергетики РН.

После определения необходимой скорости DV_необх, исходя из требований конкретной миссии мы имеем возможность определить массу топлива из уравнения 17-7 для одноступенчатых РН и раздела 17.5 – для многоступенчатых.