|
|
(9.4.2) |
В нашем случае
|
|
(9.4.3) |
где 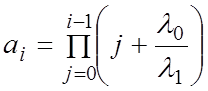 , или
, или 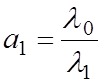 .
.
Так как по экспоненциальному закону Р=е-lt, то
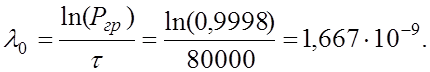
Вероятность безотказной работы модуля:

Вероятность безотказной работы всей системы после первого резервирования:
|
|
(9.4.4) |
![]()
Определим эффективность резервирования:
|
|
(9.4.5) |
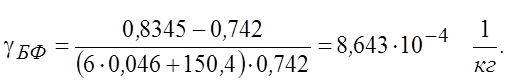
2. Добавляем резервный аккумулятор в БХ («теплый» резерв замещением).
|
где |
(9.4.6) |
В нашем случае
|
|
(9.4.7) |
|
|
(9.4.8) |
 1/с;
1/с; 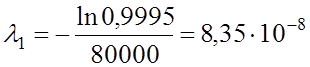 1/с.
1/с.
Тогда 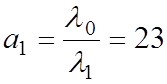 .
.
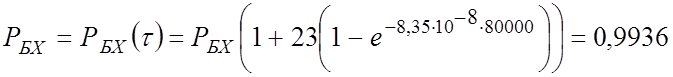 .
.
Вероятность безотказной работы всей системы
|
|
(9.4.9) |
![]()
Определим эффективность резервирования:
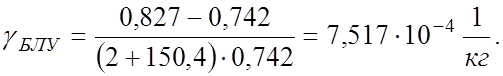
3. Добавим резервный БЛУ («холодный» резерв):
|
|
(9.4.10) |
где 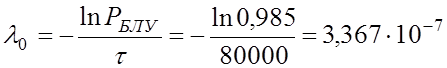 1/с.
1/с.
Тогда
![]() .
.
Вероятность безотказной работы всей системы
|
|
(9.4.11) |
![]()
Эффективность резервирования
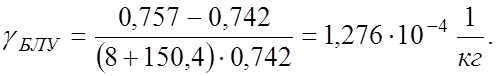
Добавлять резервные ЗРУ и РИМ нецелесообразно, так как их надежность совпадает с надежностью БЛУ, но масса больше, значит, эффективность резервирования ниже.
Выбираем то
резервирование, эффективность резервирования g
которого больше. Тогда резервируем БФ скользящим резервом с переключателем.
Получаем ![]() . Новая масса W=150,4+0,368=150,768 кг.
. Новая масса W=150,4+0,368=150,768 кг.
Полученная надежность системы ниже заданной, поэтому продолжаем резервирование.
1. Резервируем БХ. Для этого добавим еще один резервный аккумулятор. Тогда
Р/БХ=0,9935.
При этом вероятность работы всей системы
|
|
(9.4.12) |
![]()
Эффективность резервирования
|
|
(9.4.13) |
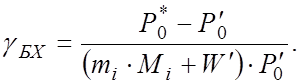
2. Резервируем БЛУ:
Р/БЛУ=0,9998;
|
|
(9.4.14) |
![]()
Эффективность резервирования
|
|
(9.4.15) |

Поскольку эффективность резерва выше при резервировании БХ, используем 24 аккумулятора. При этом новая масса системы W/=152,768 кг. Надежность Р//0=0,935 меньше заданной Рз=0,95. Продолжаем резервирование.
Дальнейшее резервирование БФ и БХ нецелесообразно, поэтому резервируем БЛУ. Если принять РБЛУ(t)=0,9998, то
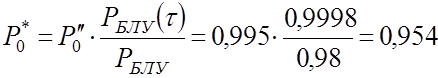 .
.
Получили необходимую надежность СЭС. Масса системы
![]() кг.
кг.
Таким образом, требования по надежности выполнены.
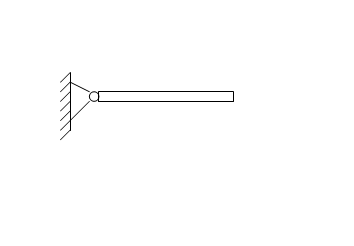 |
Рис. 9.3 Схема крепления рамы фотоэлектрической батареи
|
|
(9.4.16) |
где Е=0,7×1011 Па – модуль Юнга;
J – момент инерции сечения рамы;
l=1,78 м – длина панели БФ;
m – погонная масса панели БФ:
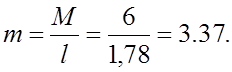
Здесь М=6 кг – масса панели БФ.
Угловую скорость раскрытия w0 найдем так:
|
|
(9.4.17) |
где j=p/2 рад – угловое перемещение панели БФ;
t – время раскрытия панели БФ:
|
|
(9.4.18) |
где К – жесткость пружины раскрытия панели БФ
(принимаем К=0,1 Н/рад).
Здесь J0 – массовый момент инерции:
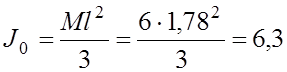 кг×м2.
кг×м2.
Тогда
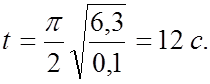
Значит,
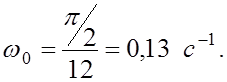
Вычислим момент инерции сечения рамы согласно рис.9.4:
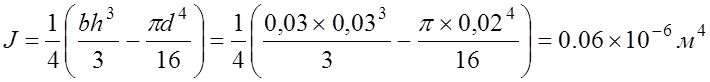 , где b=0,03 м; h=0,03
м;
, где b=0,03 м; h=0,03
м;
d=0,02 м.
Максимальный изгибающий момент

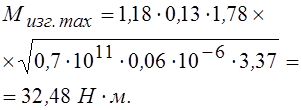
Момент сопротивления сечения
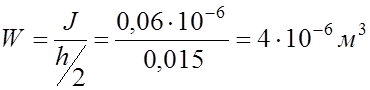 .
.
Сопротивление изгибающего момента
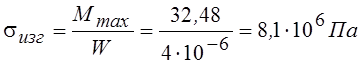 .
.
Вероятность безотказной работы вычислим по выражению
|
|
(9.4.19) |
где 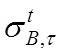 - предел длительной прочности (справочная
величина);
- предел длительной прочности (справочная
величина);
![]() - максимально действующее напряжение;
- максимально действующее напряжение;
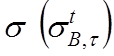 - дисперсия допустимых значений предела
длительной прочности (справочная величина);
- дисперсия допустимых значений предела
длительной прочности (справочная величина);
![]() - дисперсия допустимых значений
максимально действующего напряжения.
- дисперсия допустимых значений
максимально действующего напряжения.
Полное значение действующего напряжения определяется так:
|
|
(9.4.20) |
а дисперсии допустимых значений
|
|
(9.4.21) |
|
|
(9.4.22) |
|
|
(9.4.23) |
Подставив значения величин из (9.4.22) и (9.4.23) в
выражение (9.4.21), найдем значение дисперсии допустимых значений максимально
действующего напряжения ![]() .
.
Подставив значение ![]() и
и ![]() в выражение (9.4.19), найдем вероятность
безотказной работы.
в выражение (9.4.19), найдем вероятность
безотказной работы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.