Надежность СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ КОСМИЧЕСКОГО АППАРАТА и ее расчет, страница 2

Обратная величина вероятности безотказной работы – вероятность появления отказов (Q(t)) – связана с вероятностью безотказной работы соотношением

(9.1.2)

Интенсивность отказов представляет собой отношение числа отказавших изделий в единицу времени к среднему числу изделий, сохранивших работоспособность в промежутке времени ():

(9.1.3)

где     n(t) – число отказавших изделий за определенный промежуток времени;

N_cp(t) – среднее число изделий, сохранивших работоспособность в промежуток времени ();

(9.1.4)

Здесь N(t)– число исправно работающих изделий в начале интервала времени ();

 – число исправно работающих изделий в конце .

Поскольку рассматриваемые в теории вероятности случайные величины имеют размерность времени, то для них всегда справедливо такое равенство:

(9.1.5)

где     F – функция распределения вероятностей случайных величин.

Запишем:

;	(9.1.6)
;	(9.1.7)
,	(9.1.8)

где     F(t) – функция распределения вероятностей случайной величины;

f(t) – плотность вероятности;

G(t) – дополнительная функция распределения;

H(t) – функция интенсивности.

Из (9.1.6) – (9.1.8) вытекает функция

(9.1.9)

Каждая из перечисленных выше функций описывает закон распределения случайной величины. Таким образом, распределения случайных величин (Т, Тв, Тс, Тд), задаваемые в любой из возможных форм, являются характеристиками надежности. Так, дополнительная функция распределения случайной величины Т получила название вероятности безотказной работы. Функция интенсивности той же случайной величины называется интенсивностью отказов.

В связи с неудобством использования функций в инженерной практике широкое применение нашли числовые показатели надежности. Наиболее часто используется математическое ожидание, например, среднее время безотказной работы, среднее время восстановления, среднее время сохраняемости, средний срок службы и средний ресурс. Широко применяются значения прямой и дополнительной функций распределения для фиксированных значений времени. Используется также ряд комплексных показателей: коэффициент готовности, коэффициент простоя, коэффициент оперативной готовности (вероятность безотказной работы в течение фиксированного времени при произвольном моменте начала формирования), коэффициент технического использования (вероятность работоспособности в произвольно выбранный момент времени):

;	(9.1.10)
;	(9.1.11)
;	(9.1.12)
	(9.1.13)

где      – средняя продолжительность одного сеанса технического обслуживания;

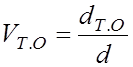 – коэффициент технического обслуживания, определяемый как отношение числа сеансов обслуживания за фиксированный интервал времени к среднему числу отказов за тот же период. Запишем выражение для вероятности безотказной работы в период нормальной эксплуатации механизмов и среднего времени безотказной работы:

	(9.1.14)
	(9.1.15)

Для большинства систем, элементы которых работают в условиях постоянства интенсивности отказов, вероятность безотказной работы может быть определена по формуле

(9.1.16)

где     P_i – вероятность безотказной работы i-го элемента, отказ которого приводит к отказу всей системы;

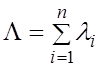 – интенсивность отказов всей системы.

Тогда среднее время безотказной работы можно вычислить так:

(9.1.17)

Значения интенсивности отказов находят опытно-статистическим путем или в литературе.

Если условия эксплуатации не соответствуют нормальным, которые определены стандартом, то при расчете интенсивности отказов системы учитывают коэффициенты нагрузки К. Отношение рабочей нагрузки к ее номинальному и рекомендуемому значению вычисляется по формуле

(9.1.18)

В настоящее время для расчета надежности механических систем нет общей методики. Это объясняется ограниченной возможностью использования стандартных деталей; отсутствием статистических данных о неисправностях деталей одинаковой конструкции вследствие различия режимов работы; быстрой сменой современных материалов, требований, технологий; непостоянством процессов разрушения.