Конструкція та розрахунок на міцність плазмово-іонної двигунної установки та системи енергопостачання, страница 8

Бак состоит из двух полусфер, приваренных аргонодуговой сваркой к силовому кольцу, на котором расположены два вида ушек.. Ферма является несущим элементом конструкции. Ферма крепится к баку, она состоит из четырех частей. Первая предназначена для крепления всей конструкции к КЛА, крепление происходит с помощью девяти болтов М6, которые ставятся в отверстия, расположенные на крестообразной части фермы. Вторая часть фермы крепится к  силовому кольцу бака с помощью четырех крепежных пластин, эта часть предназначена для того, чтоб к ней крепились остальные части фермы, к которым крепятся движители и элементы регулирования и распределения рабочего тела. Рабочее тело подается с помощью трубопроводов. Трубопровод из бака к ресиверу крепится с помощью пускового клапана, корпус которого изготовлен в виде штуцера. К ресиверу трубопровод крепится с помощью похожих электроклапанов. Ресивер, формы тора, надет на бак и крепится к ферме в четырех местах.

Силовые стержни крепления выполнены из нержавеющей стали Х18Н10Т.

Материалом  для бака является сплав Д16А, этот сплав характеризуется хорошими весовыми и прочностными характеристиками.

3.2 Расчет некоторых элементов двигательной установки

3.2.1 Расчет на прочность стенок бака

В качестве материала для бака выбираем Д16А, выбор данного материала обусловлен хорошими весовыми и прочностными характеристиками. Д16А имеет следующие прочностные и механические характеристики:

- Предел прочности,

- Предел текучести,

При расчете на прочность бака  требуется определить максимальное усилие, которое действует на стенки камеры при их максимальной температуре, до которой нагревается бак в результате воздействия солнечных лучей. Сферический бак с каким-либо рабочим газом, в условиях космического пространства может разогреваться до  за счет потока энергии солнечных лучей ( @ 1,4 кВт/м²). Охлаждение бака происходит исключительно за счет излучения теплоты в окружающую среду и определяется законом Стефана-Больцмана N=. Таким образом, можно определить максимальную температуру, до которой может нагреться бак с рабочим веществом, а, следовательно, и максимальное давление, которое возникает при этой температуре. При определении максимальной температуры бака, следует учесть, что в сбросе тепла участвует вся поверхность бака, в то время как, солнечные лучи греют лишь половину поверхности бака . Учтя всё выше сказанное уравнение теплового баланса, будет иметь вид:

(3.1)

Решение данного уравнения может определить максимальную температуру, до которой может, нагреться бак в условиях космического пространства. Решение этого уравнения имеет вид:

(3.2)

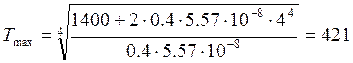К

Из уравнения Менделеева-Клапейрона, следует следующая взаимосвязь между давлением и температурой до изменения, и после изменения термодинамических параметров:

(3.3)

(3.4)

(3.5)

Определим максимальное давление, которое может действовать в баке, вследствие изменения температуры хранения рабочего вещества, при данном расчёте принимается допущение: температура рабочего вещества, хранящегося в баке, равна температуре его стенок.

(3.6)

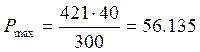 атм.

Выбрав материал бака, а, следовательно, зная его прочностные характеристики (см. выше), можно определить минимальную толщину стенки бака :

(3.7)

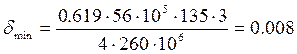мм где k – принимаемый коэффициент запаса, равный 3 из-за повышенных требований к материалам, работающим в космическом пространстве.

Из условий повышенной надёжности и используя рекомендации по изготовлению бака, толщину бака принимаем равной  м.

Зная толщину стенки бака, его геометрические размеры и плотность КМ, из которого изготавливают бак, определим его массу (плотность Д16А принимаем равной плотности алюминия):

(3.8)

 кг.

Определив массу конструкции бака и зная массу рабочего тела, определяется масса заправленного бака:

кг

(3.9)

Где  кг – масса рабочего тела, которая посчитана в курсовой работе «Основитеорії та функціювання плазмових прискорювачів»