Конструкція та розрахунок на міцність плазмово-іонної двигунної установки та системи енергопостачання, страница 10

Масса нерезервированной системы определяется по формуле:

(4.1)

где  - масса отдельных элементов, кг;

 - количество элементов, штук.

Вероятность безотказной работы нерезервированной системы определяется:

,

(4.2)

где  - вероятность отказа элемента.

Если каждый элемент системы зарезервировать  раз, то масса резервированной системы будет:

,

(4.3)

а вероятность безотказной работы:

.

(4.4)

Необходимо найти такие целые числа , при которых вероятность безотказной работы , которая определяется по (4.5), была бы максимальной, а масса  не превышала б допустимой массы , то есть:

.

(4.5)

Очевидно, что надежность будет максимальной при следующем условии:

,

(4.6)

где  - кратность резервирования.

Запишем уравнение Лагранжа:

,

(4.7)

где λ – множитель Лагранжа.

Решим это уравнение относительно . После ряда преобразований уравнение будет иметь вид:

,

(4.8)

где 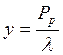, а .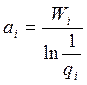

Тогда определение значения  будет иметь следующий вид:

,

(4.9)

где  - положительный корень решения уравнения  (4.9), который определяется методом последовательного приближения по выражениям:

,

(4.10)

.

(4.11)

В большинстве случаев достаточно определить второе приближение , погрешность при этом не превышает 3...5 %.

Согласно формулам (4.10) и (4.11):

;

.

Результаты расчетов сводим в таблицу:

Таблица 4.2 количество элементов одного типа

	0.01	0,003	0,003	0,003	0,007.407E-3	0,006.758E-3	0.017	0.351	0,003.058E-3	0,005.758E-3	0,005.758E-3	0,003.062E-3	0,003.062E-3
	1.645	2.1	0.961	1.957	2.379	2.218	3.344	1.305	2.1	2.218	2.218	2.803	2.803

Вычисленные значения  могут иметь любое значение, но нас интересуют , которые дают максимум функции  и удовлетворяют условию  ().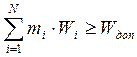

Среди целых чисел, которые отличаются от  не больше, чем на единицу, следует выбирать такие, при которых в сравнении с другими возможными системами целых чисел удовлетворялись бы два условия:

,

(4.12)

.

(4.13)

В таблицу 4.3: „а” – округленное до целого числа, „б” – округлено влево, „в” – округлено вправо.

Таблица 4.3 – количество элементов одного типа.

а	2	2	1	2	2	2	3	1	2	2	2	3	3
б	1	2	1	1	2	2	3	1	2	2	2	2	2
в	2	3	1	2	3	3	4	2	3	3	3	3	3

Проверяем условие (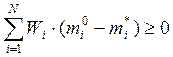). Из трех вариантов оптимальным является вариант „б”. Тогда, по формуле (4.5) определяем вероятность безотказной работы резервированной системы:

Массу резервированной системы определяем по формуле (4.5):

кг.

Условие (4.6) выполняется:

.

5 РАСЧЕТ ФИЗИЧЕСКОЙ НАДЕЖНОСТИ УСКОРЯЮЩЕГО ЭЛЕКТРОДА ИОС

Ускоряющий электрод ИОС изготовлен из молибдена

Для определения физической надежности ускоряющего электрода ИОС можно воспользоваться следующей формулой:

,

(5.1)

где -предел длительной прочности материала ускоряющего электрода ИОС  МПа;

-эквивалентное напряжение в наиболее нагруженной точке,  МПа;