Другие предметы \ Конструирование несущих элементов конструкции

Конструкція та розрахунок на міцність плазмово-іонної двигунної установки та системи енергопостачання, страница 7

Рис 2.3 Cхема расчета на прочность ускоряющего электрода, методом сил.

Принимаем, что радиальная деформация в точке С электрода равна радиальной деформации кольца.

(2.1)

(2.2)

Где - сила от температуоного нагревания;

, - температурные деформации,

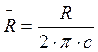- распределенная сила, Н.

Если сетка цельная, то для нее можно записать:

(2.3)

(2.4)

Податливость и найдем условно принимая, что (как бы забываем про температурные напряжение):

(2.5)

(2.6)

В точке С относительная деформация будет:

(2.7)

Деформацию от силы можно записать так:

(2.8)

где - напряжения от силы , МПа.

(2.9)

(2.10)

Тогда с учетом выражений (2.8), (2.9), (2.10) податливость можно переписать так:

(2.11)

(2.12)

Теперь из выражения (2.2) можно найти :

(2.13)

С учетом раньше записанных и , можем записать для нашего случая так:

(2.14)

(2.15)

где - напряжения от силы , МПа.

Величина находится так:

(2.16)

где - толщина не перфорированной пластины, прогиб которой равняется прогибу перфорированной пластины.

(2.17)

(2.18)

(2.19)

где - диаметр отверстий в электроде ИОС, мм;

- шаг между отверстиями в электроде ИОС, мм.

Тогда,

(2.20)

(мм),

(2.21)

Найдя и , находятся эквивалентные напряжения:

(2.22)

Расчет проведен в программе, написанной в MathCADe (Приложение 1), в результате получено распределение напряжений по радиусу электрода, что изображено на рис 2.5

мм

Рис 2.5 график распределения вдоль радиуса электрода

Максимальное напряжение будет при :

(МПа),

Коэффициент запаса прочности для сетки будет равен:

(2.23)

где МПа – предел длительной прочности материала молибден.

Так, как коэффициент запаса прочности получился маленьким, то необходимо увеличить толщину электрода на 0,3 мм.

Определим критические напряжения, при которых сетка потратит устойчивость:

МПа

(5.24)

Если

(5.25)

То сетка будет устойчивой.

В нашем случае условие (5.25) не выполняется , т.е сетка не устойчива, поэтому в конструкции ИОС мы создали направление для деформации, выгнув пластины в одном направлении, чтобы сетки не соприкасались..