Решение задач по теме: "Комбинаторика"

3. КОМБИНАТОРИКА

Задача 20. В спортивном магазине было куплено 1000 пар лыж, 500 пар ботинок и 500 пар лыжных палок. При этом 400 пар лыж куплено вместе с ботинками, 300 пар лыж вместе с палками, 200 пар ботинок вместе с палками, а 100 пар лыж – вместе с ботинками и палками. Сколько человек сделали покупки?

Решение.

Введем обозначения:

 – множество людей, купивших лыжи,

 – число людей, купивших лыжи, =1000;

 – множество людей, купивших ботинки,

 – число людей, купивших ботинки, =500;

 – множество людей, купивших палки,

 – число людей, купивших палки, =500;

 – множество людей, купивших лыжи и ботинки,

 – число людей, купивших лыжи и ботинки, =400;

 – множество людей, купивших лыжи и палки,

 – число людей, купивших лыжи и палки, =300;

 – множество людей, купивших ботинки и палки,

 – число людей, купивших ботинки и палки, =200;

 – множество людей, купивших лыжи, ботинки и палки,

 – число людей, купивших лыжи ботинки и палки,

=100;

 – множество людей, сделавших покупки,

 – число людей, сделавших покупки.

Применяя правило суммы для трех пересекающихся множеств:

,

получаем:

=1000+500+500-400-300-200+100=1200.

Ответ. 1200 человек сделали покупки.

Задача 21. Из урны, в которой лежат 5 красных и 6 белых шаров, вынимают наугад три шара (без возвращения). Сколько существует возможностей вынуть три белых шара? Три красных? Два белых и один красный?

Решение.

Введем обозначения:

n(Б) – число возможностей вынуть первым белый шар, n(Б)=6;

n(Б|Б) – число возможностей вынуть вторым белый шар, если первый шар был белым, n(Б|Б)=5;

n(Б|ББ) – число возможностей вынуть третий белый шар, если первый и второй были белыми, n(Б|ББ)=4;

n(К) – число возможностей вынуть первым красный шар, n(К)=5;

n(К|К) – число возможностей вынуть вторым красный шар, если первый шар был красным, n(К|К)=4;

n(К|КК) – число возможностей вынуть третий красный шар, если первый и второй были красными, n(К|КК)=3;

n(К|ББ) – число возможностей вынуть красный шар третьим, если первый и второй были белыми, n(К|ББ)=5.

Используя правило произведения, получаем:

1) число возможностей вынуть три белых шара

n(Б)·n(Б|Б)·n(Б|ББ) = 6·5·4 = 120,

2) число возможностей вынуть три красных шара:

n(К) · n(К|К) · n(К|КК) = 5·4·3 = 60.

3) При вычислении числа возможностей вынуть два белых и один красный шар необходимо учитывать, что эти возможности могут реализоваться в трех различных вариантах: ББК (белый, белый, красный), БКБ и КББ.

Для первого варианта (ББК) число возможностей равно:

n(Б)·n(Б|Б)· n(К|ББ) = 6·5·5 = 150.

Второй и третий варианты по числу возможностей не отличаются от первого и тоже дают по 150 возможностей. Следовательно, общее число возможностей вынуть 2 белых и один красный шар равно 150·3=450.

Задача 22. Пусть "счастливый" билет в автобусе – это билет, в котором сумма первых трех цифр равна сумме последних трех цифр. Сколько существует "счастливых" билетов, в которых первая сумма составлена из цифр 1,3,7, а вторая – из 0,2,5?

Решение.

Будем решать задачу по действиям.

1. Найдем, сколько трехзначных чисел можно составить из заданных цифр. Для этого определим вид расстановок, которые являются такими числами. Ответим на вопросы схемы определения вида расстановок.

а) Расстановки отличаются составом элементов (например, 113, 137). Расстановки являются размещениями или сочетаниями.

б) Расстановки отличаются порядком элементов (например, 113 и 131), Расстановки являются размещениями.

в) Элементы в расстановках повторяются (например, 337). Расстановки есть размещения с повторениями из трех элементов по три элемента.

Число таких размещений .

2. Составим по 27 чисел из заданных троек цифр и выделим клетки "счастливых" билетов. Решение оформим в виде таблиц (табл.1 и табл. 2).

Табл.1 Числа, составленные из цифр 1,3,7
В старшем разряде 1	111	113	117	131	133	137	171	173	177
Сумма цифр	3	5	9	5	7	11	9	11	15
В старшем разряде 3	311	313	317	331	333	337	371	373	377
Сумма цифр	5	7	11	7	9	13	11	13	17
В старшем разряде 7	711	713	717	731	733	737	771	773	777
Сумма цифр	9	11	15	11	13	17	15	17	21

Табл.2 Числа, составленные из цифр 0,2,5
В старшем разряде 0	000	002	005	020	022	025	050	052	055
Сумма цифр	0	2	5	2	4	7	5	7	10
В старшем разряде 2	200	202	205	220	222	225	250	252	255
Сумма цифр	2	4	7	4	6	9	7	9	12
В старшем разряде 5	500	502	505	520	522	525	550	552	555
Сумма цифр	5	7	10	7	9	12	10	12	15

3. Выпишем в табл. 3 совпадающие суммы, составленные из цифр 1,3,7 и цифр 0,2,5, посчитав число одинаково закрашенных клеток в таблицах 1 и 2.

4. Введем обозначения:

, , ,  – числа "счастливых" билетов, в которых сумма первых трех цифр и вторых трех цифр равна 5, 7, 9 и 15 соответственно;

, , ,  – количество чисел, составленных из цифр 1,3,7, сумма цифр которых равна 5, 7, 9, 15 соответственно;

Аналогично , , ,  – количество чисел, составленных из цифр 0,2,5, сумма цифр которых равна 5, 7, 9 и 15.

В этих обозначениях по правилу произведения имеем:

=·=3·3=9;

=·=3·6=18;

=·=4·3=12;

=·=2·1=2.

Число всех "счастливых" билетов, удовлетворяющих условию задачи, по правилу суммы равно: +++=9+18+12+2=41.

Задача 23. Сколькими способами можно распределить комнаты в четырехкомнатной квартире между 1) четырьмя, 2) тремя, 3) пятью ее обитателями?

Решение.

Пусть  – множество номеров комнат в квартире,

 – множество жильцов квартиры, если их четверо,  – множество жильцов, если их трое, и  – если их пятеро.

Распределение комнат между жильцами можно представить как присваивание номера комнаты каждому жильцу. Например, если жильцов четверо, то некоторые варианты расселения их по комнатам можно представить в виде таких двустрочных матриц:

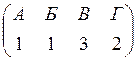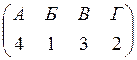, или , или 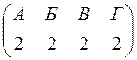 и т.п.

Двустрочные матрицы представляют собой расстановки из четырех элементов (номеров комнат) по четырем позициям (именам жильцов).