4. БУЛЕВЫ ФУНКЦИИ
Задача 30. Докажите
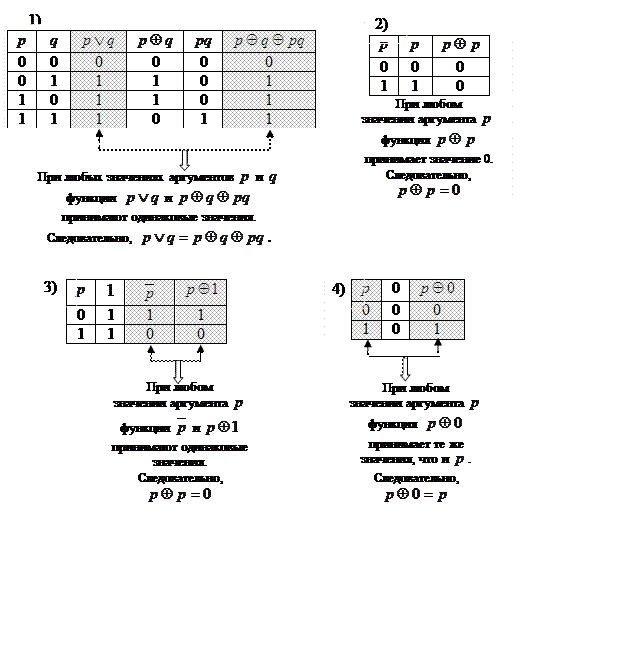
с помощью таблиц следующие свойства операции кольцевая сумма: 1) ![]() , 2)
, 2) ![]() , 3)
, 3)
![]() , 4)
, 4) ![]() .
.
Решение.
|
|
|
|
Используя определение кольцевой суммы, записанное в табличной форме, составим таблицы, подтверждающие каждое из равенств. |
|
0 |
0 |
0 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
0 |
 |
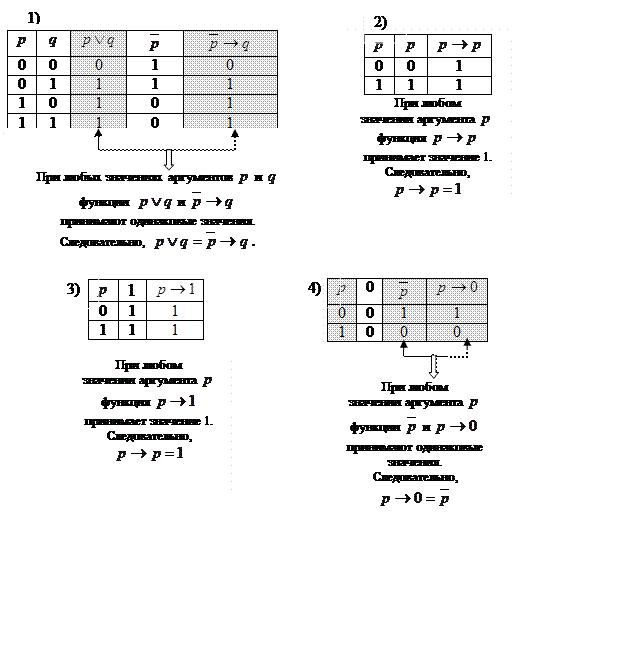
Задача 31. Докажите с помощью таблиц следующие свойства операции
импликация: 1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() ,
4)
,
4) ![]() .
.
Решение.
|
|
|
|
Используя определение импликации, записанное в табличной форме, составим таблицы, подтверждающие каждое из равенств. |
|
0 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
Задача 32.
Запишите функции ![]() и
и ![]() ,
используя
,
используя
1) операции кольцевая сумма и конъюнкция, 2) операции импликация, конъюнкция и отрицание.
Решение.
1) Используя равенства ![]() ,
,
![]() , выполним преобразование дизъюнкций
, выполним преобразование дизъюнкций ![]() и
и ![]() в
кольцевые суммы.
в
кольцевые суммы.
![]()
![]() ;
;
![]() ;
;
Равенство (*) основано на свойстве конъюнкции: ![]() .
.
2) Используя равенство ![]() ,
выполним преобразования дизъюнкций в импликации.
,
выполним преобразования дизъюнкций в импликации.
![]()
В преобразованиях использованы свойства булевых операций:
(1) двойственность ![]() ,
,
(2) двойное отрицание ![]() .
.
![]() .
.
Задача 33. Установите
равенство или неравенство булевых функций ![]() и
и
![]() .
.
Решение.
Составим таблицы функций ![]() и
и
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
Поскольку на некоторых наборах значений аргументов ![]() и
и ![]() принимают
разные значения (выделено цветом), функции не равны друг другу
принимают
разные значения (выделено цветом), функции не равны друг другу ![]()
![]() .
.
Задача 34.
Исключите из формулы ![]() фиктивные переменные, если
они имеются.
фиктивные переменные, если
они имеются.
Решение.
Используя операцию дизъюнкции, исключим из формулы операции импликации и кольцевой суммы. Далее, используя свойства операций конъюнкции, дизъюнкции и отрицания, упростим полученную формулу.
![]()
![]()
![]() .
.
Вывод: все аргументы
функции ![]() являются фиктивными, так как при
любых значениях переменных
являются фиктивными, так как при
любых значениях переменных ![]() .
.
При упрощении формулы использованы следующие свойства операций:
(1) преобразование импликации в дизъюнкцию ![]() ;
;
(2) двойное отрицание ![]() ;
;
(3) дистрибутивность конъюнкции относительно
дизъюнкции ![]() ;
;
(4) закон исключения третьего ![]() ;
;
(5) свойство единицы для конъюнкции ![]() .
.
Задача 35. Булева
функция четырех переменных задана таблицей. Составьте СДНФ и СКНФ функции ![]() .
.
Решение.
Запишем в последнем столбце таблицы элементарные конъюнкции и дизъюнкции, применяя следующие правила:
1) Элементарные конъюнкции записываются для единичного набора функции, элементарные дизъюнкции – для нулевого набора.
2) В каждую элементарную конъюнкцию или дизъюнкцию входят все аргументы функции либо сами по себе, либо своими отрицаниями.
3) В элементарную конъюнкцию отрицаниями входят аргументы, принимающие в данной строке таблицы значение нуль; в элементарную дизъюнкцию отрицаниями входят аргументы, принимающие в данной строке таблицы значение единица.
|
|
|
|
|
|
Элементарные конъюнкции и дизъюнкции |
|
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
|
|
1 |
0 |
1 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
0 |
|
Соединив все элементарные конъюнкции знаками
дизъюнкции, получим СДНФ функции ![]() :
:
СДНФ(![]() )=
)=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Соединив все элементарные дизъюнкции знаками конъюнкции,
получим СКНФ функции ![]() :
:
СКНФ(![]() )=
)=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Задача 36.
Упростите СДНФ(![]() ) (задача 35) с помощью
карты Карно и таблицы Куайна.
) (задача 35) с помощью
карты Карно и таблицы Куайна.
Решение.
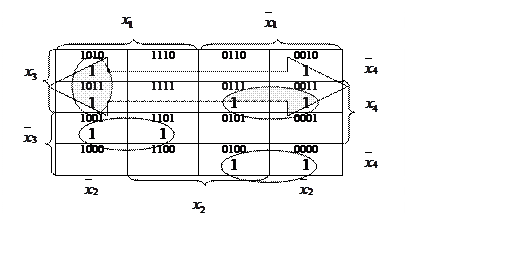 |
При использовании карты Карно надо выполнять следующие правила:
1) Знаком "1" помечают клетки, соответствующие единичному набору функции. Нули функции в карту не заносят.
2) Объединяют 2,4,8…2n стоящих рядом помеченных клеток.
3) Каждое объединение представляет одну компоненту ДНФ функции.
4) В компоненте сохраняются те переменные, которые не изменяются в объединенных клетках.
Пользуясь правилами 1-4, запишем упрошенную формулу
функции ![]() :
:
КНФ(![]() )=
)=![]() .
.
Составим таблицу Куайна для полученной КНФ.
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
* |
* |
* |
|||||
|
|
* |
* |
|||||||
|
|
* |
* |
* |
||||||
|
|
* |
* |
|||||||
|
|
* |
* |
* |
При использовании таблицы Куайна надо выполнять следующие правила:
1) Столбцы в таблице соответствуют элементарным конъюнкциям в СДНФ, строки – конъюнкциям в упрощенной ДНФ.
2) В каждой строке помечаются клетки, в которых конъюнкция из ДНФ входит в элементарную конъюнкцию СДНФ (покрывает элементарную конъюнкцию).
3) Если в столбце несколько меток, то соответствующая элементарная конъюнкция покрыта несколькими конъюнкциями ДНФ, если одна – только одной конъюнкцией. Каждая элементарная конъюнкция из СДНФ должна быть покрыта хотя бы один раз. Помечаем цветом те столбцы таблицы, в которых имеется два и более покрытий.
4) Если все помеченные клетки какой либо строки оказываются закрашенными, строка может быть вычеркнута из ДНФ
5) После вычеркивания одной строки вновь производится закрашивание клеток и процедура повторяется.
Пользуясь правилами 1-3, заполним таблицу Куайна и отметим
цветом столбцы, содержащие более одной метки. В соответствии с правилом 4,
можно вычеркнуть первую или вторую строки таблицы. Вычеркнув вторую строку,
получим упрощенную ДНФ функции ![]() :
:
![]() =
=![]() .
.
После удаления второй строки и повторного закрашивания клеток, можно видеть, что каждая строка содержит хотя бы по одной незакрашенной клетке. Следовательно процедура упрощения ДНФ закончена.
Задача 37.
Преобразуйте формулу ![]() =
=![]() в
кольцевую сумму.
в
кольцевую сумму.
Решение.
Воспользуемся формулами перехода от дизъюнкции и
отрицания к кольцевой сумме: ![]() ,
, ![]() .
.
Преобразования будем выполнять по действиям:
1. ![]()
![]()
![]()
![]()
![]() ;
;
2. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
3. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
4. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
В действиях 1-3 выполнен переход от дизъюнкции к кольцевой сумме. В действии 4 сделана замена отрицаний переменных.
Задача 38. Булева функция трех переменных задана единичными наборами:
![]() : (0,3,5,7). Запишите таблицу этой
функции, представьте ее в алгебрах
: (0,3,5,7). Запишите таблицу этой
функции, представьте ее в алгебрах ![]() и
и ![]() .
.
Решение.
Запишем таблицу функции и элементарные конъюнкции ее СДНФ.
|
|
|
|
|
Элементарные конъюнкции |
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
|
СДНФ (![]() )=
)=![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Упростим формулу СДНФ, пользуясь свойствами булевых операций:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Преобразуем формулу ![]()
![]() к
кольцевой сумме:
к
кольцевой сумме:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Ответ. В
алгебре ![]() функция
функция
![]() имеет формулу:
имеет формулу: ![]() :
:
В алгебре ![]() функция
функция
![]() может быть записана формулой
может быть записана формулой
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.