1. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
Задача 1.
Представить множества ![]() ,
, ![]() ,
,
![]() ,
, ![]() на
диаграмме Эйлера-Венна.
на
диаграмме Эйлера-Венна.
Решение.
Поскольку множества ![]() ,
, ![]() и
и
![]() являются подмножествами множества
являются подмножествами множества ![]() , выберем в качестве универсального
множества множество
, выберем в качестве универсального
множества множество ![]() .
.
Диаграмма Эйлера-Венна выглядит следующим образом:
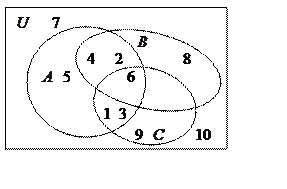 |
Задача 2. Записать
характеристические функции множеств ![]() ,
, ![]() и
и ![]() (задача
1) в виде двоичных векторов. Пронумеровать каждую область диаграммы
Эйлера-Венна двоичным номером.
(задача
1) в виде двоичных векторов. Пронумеровать каждую область диаграммы
Эйлера-Венна двоичным номером.
Решение.
Так как универсальным множеством является множество ![]() , содержащее 10 элементов,
характеристические функции его подмножеств могут быть представлены
десятимерными двоичными векторами. Последовательность координат таких векторов соответствуют
последовательности элементов множества
, содержащее 10 элементов,
характеристические функции его подмножеств могут быть представлены
десятимерными двоичными векторами. Последовательность координат таких векторов соответствуют
последовательности элементов множества ![]() .На
каждом подмножестве координата вектора принимает значение 1, если элемент
принадлежит подмножеству, и значение 0, если не принадлежит.
.На
каждом подмножестве координата вектора принимает значение 1, если элемент
принадлежит подмножеству, и значение 0, если не принадлежит.
Следовательно,
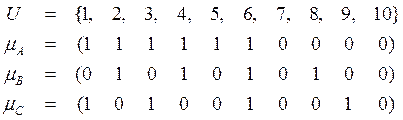 .
.
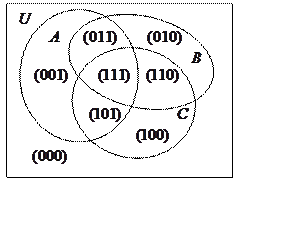 |
Задача 3. Составить
булеан множества ![]() . Записать таблицу характеристических
функций каждого множества.
. Записать таблицу характеристических
функций каждого множества.
Решение. Множество ![]() содержит
четыре элемента, следовательно его булеан содержит 24=16 подмножеств.
содержит
четыре элемента, следовательно его булеан содержит 24=16 подмножеств.
Составим таблицу элементов булеана и их характеристических функций. При записи характеристических функций используем лексикографический метод записи последовательности двоичных векторов.
|
Подмножества
множества (элементы булеана) |
Значения характеристических функций подмножеств |
|||
|
Элементы
множества |
||||
|
2 |
4 |
6 |
8 |
|
|
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
Задача
4. Составить
диаграмму отношения включения на булеане множества ![]() и
ее дерево путей. Записать все последовательности включений элементов булеана.
и
ее дерево путей. Записать все последовательности включений элементов булеана.
Решение. Диаграмма отношений включения между
элементами булеана имеет 4 уровня: уровень 0 – пустое множество,
характеристическая функция (0000), уровень 1 – множества, содержащие один
элемент, уровень 2 – множества содержащие 2 элемента, уровень 3 – множества,
содержащие 3 элемента, уровень 4 – множество ![]() ,
характеристическая функция (1111) (см. задачу 3).
,
характеристическая функция (1111) (см. задачу 3).
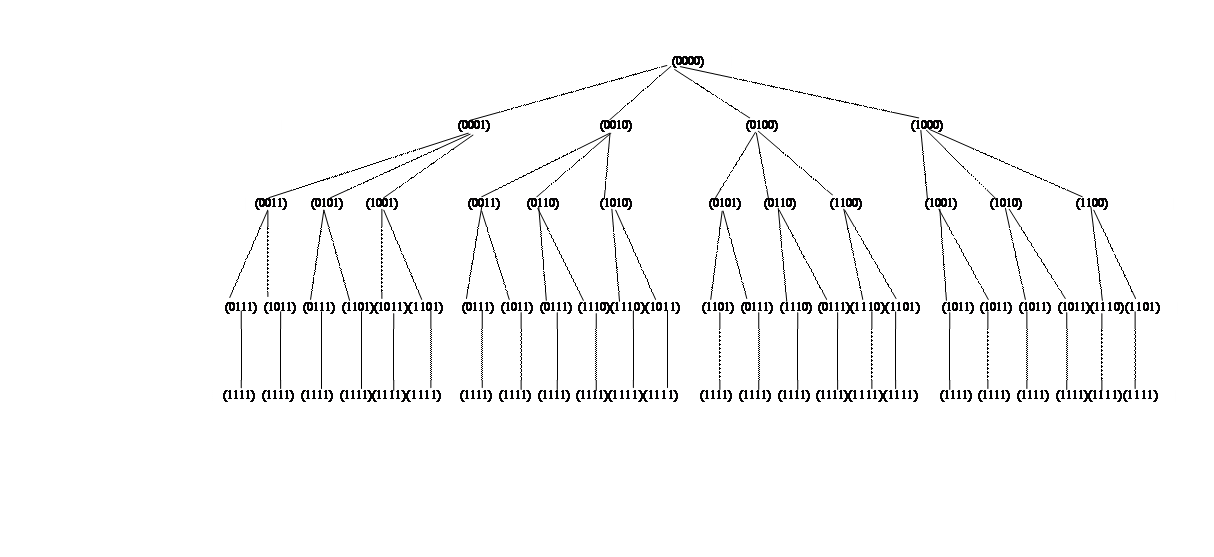
Множества одного уровня несравнимы между собой по отношению включения, но двигаясь по любому пути диаграммы, получаем последовательную цепочку включений.
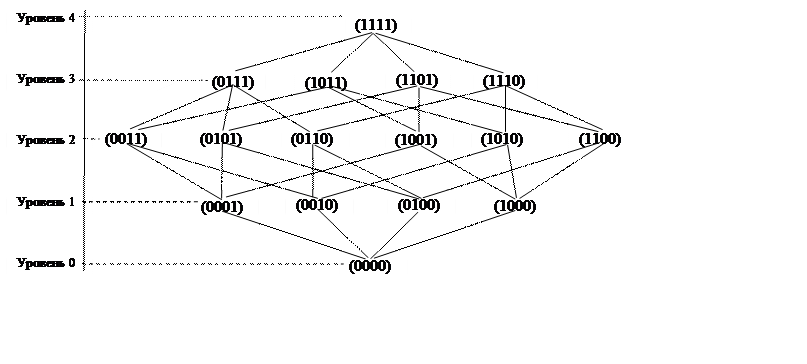
Составим дерево путей по
диаграмме включений (см. рис. стр.)
От нулевого уровня имеются четыре пути к множествам первого уровня. От каждого множества первого уровня имеется три пути к множествам второго уровня. От каждого множества второго уровня имеется два пути к множествам третьего уровня и от них по одному пути к множеству четвертого уровня.
Таким образом из 16
элементов булеана множества ![]() можно составить 24 различных
последовательности множеств, упорядоченных отношением включения. Запишем эти
последовательности.
можно составить 24 различных
последовательности множеств, упорядоченных отношением включения. Запишем эти
последовательности.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Задача 5. Доказать
равенства: ![]() ,
, ![]() ,
где
,
где ![]() и
и ![]() –
подмножества какого-либо универсального множества
–
подмножества какого-либо универсального множества ![]() .
.
Решение.
Рассмотрим любой элемент ![]() универсального
множества
универсального
множества ![]() . Используя определения операций над множествами,
запишем в таблицу все возможные варианты принадлежности и непринадлежности
. Используя определения операций над множествами,
запишем в таблицу все возможные варианты принадлежности и непринадлежности ![]() каждому из множеств. При этом
принадлежность элемента множеству будем обозначать единицей, непринадлежность –
нулем.
каждому из множеств. При этом
принадлежность элемента множеству будем обозначать единицей, непринадлежность –
нулем.
Докажем равенство ![]() .
.
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
Как видно из таблицы элемент ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() . Следовательно, равенство
. Следовательно, равенство
![]() справедливо для любых подмножеств
множества
справедливо для любых подмножеств
множества ![]() .
.
Докажем равенство ![]() .
.
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
Как видно из таблицы элемент ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() . Следовательно, равенство
. Следовательно, равенство
![]() справедливо для любых подмножеств
множества
справедливо для любых подмножеств
множества ![]() .
.
Задача 6. Подмножества
![]() и
и ![]() множества
множества
![]() заданы характеристическими функциями:
заданы характеристическими функциями:
![]() ,
, ![]() .
.
Требуется:
1) Записать списки элементов множеств ![]() и
и ![]() ;
;
2) Выполнить над множествами ![]() и
и
![]() операции:
операции: ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , используя их характеристические
функции.
, используя их характеристические
функции.
3) Записать списки элементов всех полученных множеств.
Решение.
1) Запишем списки элементов множеств ![]() и
и ![]() ,
используя определение характеристической функции множества:
,
используя определение характеристической функции множества:
![]() ,
, ![]() .
.
2) Используя правила выполнения операций над множествами, выполним все указанные в задаче действия.
![]() ;
; ![]() .
.
![]() ;
; ![]() .
.
![]() =
=![]() ;
;
![]() .
.
![]() =
=![]() ;
;
![]() .
.
![]() (см. задачу 5).
(см. задачу 5).
![]()
=![]() ;
;
![]() .
.
![]() (см.
задачу 5).
(см.
задачу 5).
![]() =
=![]() ;
;
![]() .
.
![]() (см. задачу 5).
(см. задачу 5).
![]() =
=
=![]()
![]()
![]() ;
; ![]() .
.
![]()
![]() ,
,
![]() . В равенстве
. В равенстве ![]() использовано
свойство дополнения
использовано
свойство дополнения ![]() .
.
Задача 7.
Найти множество ![]() через известные множества
через известные множества ![]() ,
, ![]() ,
если известно, что
,
если известно, что 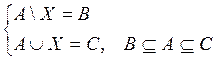 .
.
Решение. Построим
таблицу принадлежности произвольного элемента ![]() универсального
множества каждому из множеств, записанных в системе.
универсального
множества каждому из множеств, записанных в системе.
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
В таблице отмечены цветом те строки, которые соответствуют нарушению равенств системы. Выпишем строки, соответствующие системе:
|
|
|
|
|
Как видно из таблицы, элемент
|
|
|
0 |
0 |
0 |
0 |
||
|
0 |
0 |
1 |
1 |
|
|
|
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
1 |
0 |
Задача
8. Решить уравнение ![]() .
.
Решение. Применим метод решения, использованный задаче 7.
|
|
|
|
|
Из двух последних строк
таблицы очевидно, что элемент, взятый из пересечения множеств Следовательно, данное уравнение не имеет решений. |
|
|
0 |
0 |
0 |
0 |
||
|
0 |
0 |
1 |
1 |
||
|
0 |
1 |
0 |
0 |
||
|
0 |
1 |
1 |
1 |
||
|
1 |
0 |
0 |
1 |
||
|
1 |
0 |
1 |
1 |
||
|
1 |
1 |
0 |
1 |
|
|
|
1 |
1 |
1 |
1 |
|
|
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.