Решение задач по теме: "Бинарные отношения"

2. БИНАРНЫЕ ОТНОШЕНИЯ

Задача 9. Бинарное отношение  на множестве  задано характеристическим свойством .

Требуется:

1) Составить список элементов множества .

2) Составить график, матрицу инциденций и граф отношения.

Решение.

1)  (всего 49 пар элементов).

2)  – график отношения.

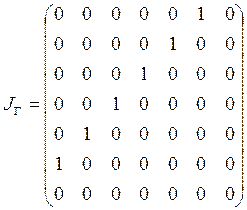 – матрица инциденций отношения.

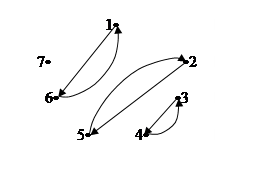
– граф отношения.

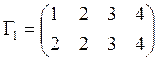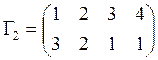Задача 10.  Бинарные отношения  на множестве  заданы двустрочными матрицами: ,  и 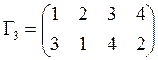. Найти расстояния между этими отношениями, используя формулы линейного и евклидова расстояния.

Решение. Запишем матрицы инциденций этих отношений:

, , .

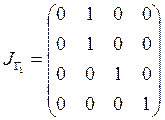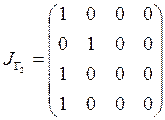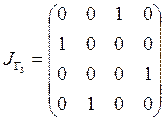Линейное расстояние между отношениями находим по формуле:

,

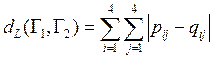евклидово расстояние:

,

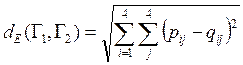где ,  элементы матриц , .

Очевидно, что , а поэтому

Получаем:

;

.

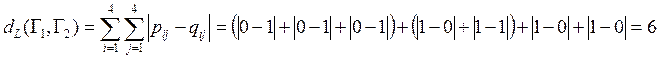Аналогично:

;

.

;

.

Задача 11. Бинарные отношения  и  на множестве  заданы характеристическими свойствами ,  .

Требуется:

1) записать матрицы инциденций этих отношений,

2) найти композиции  и ,

3) проиллюстрировать решение с помощью графов.

Решение.

1) Прежде, чем записывать матрицы инциденций отношений, выпишем их графики:

,

.

По графикам запишем матрицы инциденций:

, .

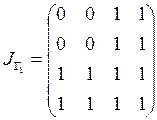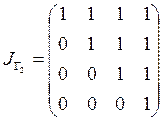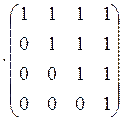
2) Композиции  и  найдем, перемножив матрицы  и  по правилу максимина:

, где  и  - элементы матриц  и ,  - элемент произведения матриц.

,

.

3) Представим отношения  и  с помощью двудольных графов.

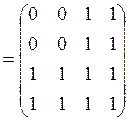
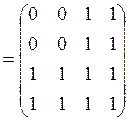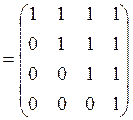
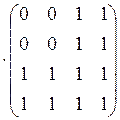
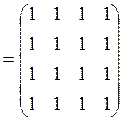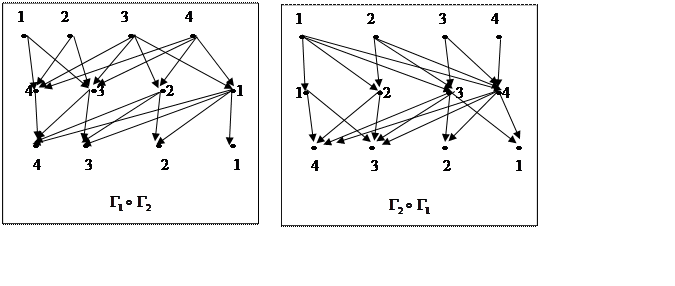Задача 12. На множестве  заданы бинарные отношения:  и . Требуется определить, какое из них  является транзитивным.

Решение.

Запишем матрицы инциденций отношений:

, .

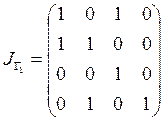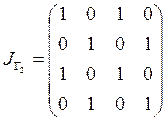Отношение транзитивно, если квадрат его матрицы инциденций не больше самой матрицы: .

Будем возводить в квадрат матрицы инциденций отношений  и  и сравнивать полученные результаты с самими матрицами инциденций.

.

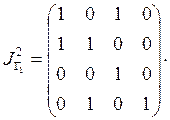
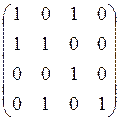
Вторая и четвертая строки матрицы  больше соответствующих строк  матрицы , т.е. . Следовательно, отношение  не является транзитивным.

.

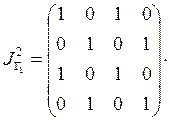
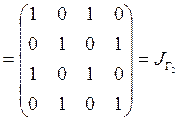Поскольку , отношение  транзитивно.

Задача 13. Для отношения  в задаче 12 выявить опосредованные связи между элементами множества .

Решение.

Вычтем из матрицы   матрицу :

.

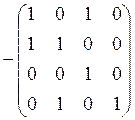
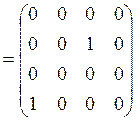В матрице  ненулевыми являются элементы  и . Следовательно, отношение  не учитывает связи между элементами (2,3) и (4,1).

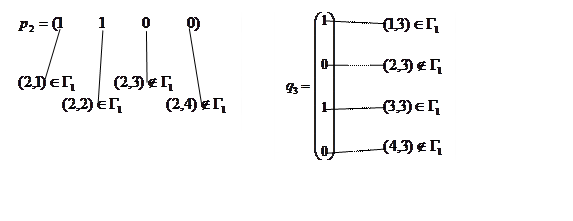
Рассмотрим опосредованные связи между элементами 2 и 3. Для этого запишем, как был получен элемент , т.е. процесс умножения второй строки матрицы  на ее третий столбец.

Сначала выпишем вторую строку и третий столбец матрицы  и покажем смысл каждого элемента.

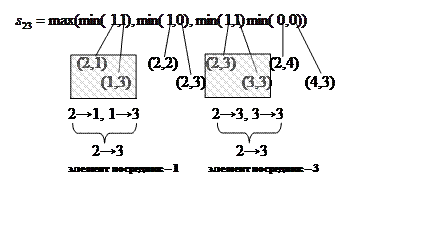Теперь распишем процесс получения , указывая смысл чисел, над которыми выполняются операции минимум и максимум.

Из рисунка видно, что опосредованная связь между элементами 2 и 3 в отношении  осуществляется элементами 1 или 3.

Таким образом, элементы-посредники, осуществляющие опосредованную связь между 2 и 3 в отношении , – это элементы 1 или 3.

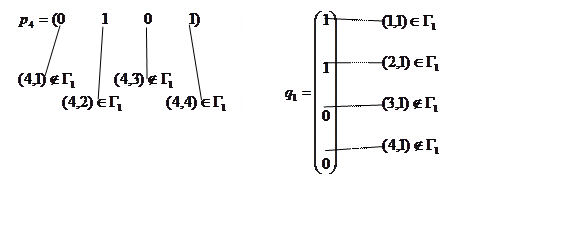
Рассмотрим опосредованные связи между элементами 4 и 1. Запишем, как был получен элемент .

Выпишем четвертую строку и первый столбец матрицы  и покажем смысл каждого элемента.

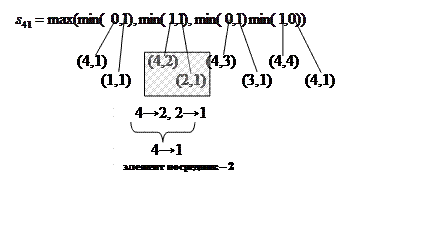Распишем процесс получения , указывая смысл чисел, над которыми выполняются операции минимум и максимум.

Из рисунка видно, что опосредованная связь между элементами 4 и 1 в отношении  осуществляется элементом 2.

Таким образом, элемент-посредник, осуществляющий опосредованную связь между 4 и 1 в отношении , – это элемент 2.

Задача 14.  Бинарное отношение  на множестве  задано матрицей инциденций:

.

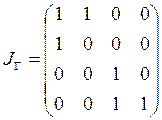Требуется:

1) Найти транзитивное замыкание отношения .

2) Найти евклидово расстояние между отношением  и его транзитивным замыканием.

3) Построить графы всех полученных отношений.

Решение.

1) Для получения транзитивного замыкания будем получать последовательность степеней матрицы .

;

;

.

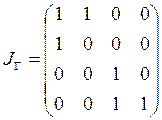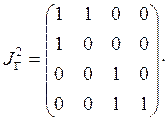
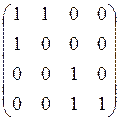
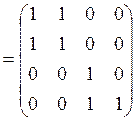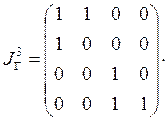
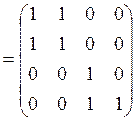
Дальнейшее умножение матриц не даст новых результатов.

Вывод: транзитивным замыканием отношения  является отношение .

2) Найдем евклидово расстояние между отношениями  и .

.

3) Построим графы отношений  и .

Задача 15. На плоскости заданы пять прямых:

,, , , .

На множестве прямых  задано отношение :"прямая  параллельна или совпадает с прямой ", .

Требуется:

1) Доказать, что  является отношением эквивалентности.

2) Записать фактор множество /.

3) Записать характеристические функции каждого класса.

Решение.

1) Напомним, что две прямые параллельны или совпадают тогда и только тогда, когда их угловые коэффициенты равны.

Перепишем уравнения прямых , , , ,  в виде уравнений прямых с угловым коэффициентом и начальной ординатой:

,     ,     ,

,     .

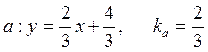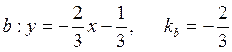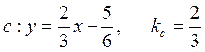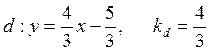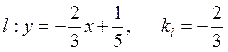Сравнение угловых коэффициентов прямых позволяет записать график отношения :

.

Запишем матрицу отношения :

.

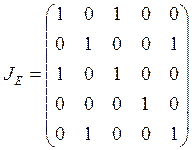а) Все элементы главной диагонали матрицы  единицы, следовательно,  – рефлексивное отношение.

б) Матрица  симметрична относительно главной диагонали, следовательно,  – симметричное отношение.

в) Для проверки транзитивности отношения найдем матрицу :

.

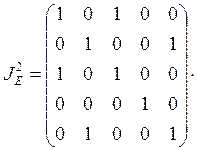
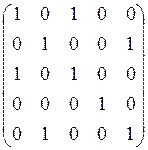
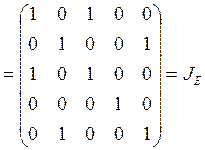, следовательно,  – транзитивное отношение.

Отношение  рефлексивно, симметрично и транзитивно, следовательно  – отношение эквивалентности.

2) Отношение эквивалентности  разбивает множество  на непересекающиеся классы эквивалентности, объединение которых составляет все множество . В один класс попадают элементы, связанные друг с другом отношением , в разные классы – этим отношением не связанные.

Перебирая элементы множества , и записывая их образы и прообразы в отношении , получим классы эквивалентности:

;

;

.

Отсюда получаем:

/.

3) Характеристические функции каждого класса запишем в виде пятимерных двоичных векторов:

, , .

Задача 16.  На множестве  задано отношение :

.

Определить, какими свойствами обладает отношение .

Решение.

а) Отношение  рефлексивно, так как на главной диагонали матрицы  все числа – единицы.

б) Отношение  не является симметричным, т.к. матрица  не симметрична относительно главной диагонали.

Проверим выполнение признака антисимметричности отношения : .

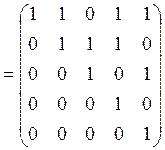
Пересечение матриц инциденций находим по правилу логического произведения: , где , , .

.

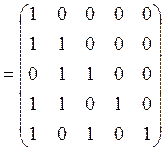
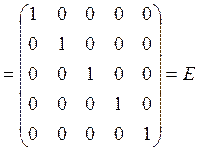Поскольку равенство  выполняется, отношение   антисимметрично.

в) Для проверки транзитивности найдем матрицу :

.

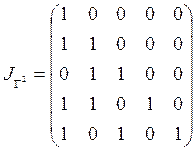
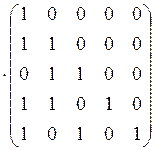
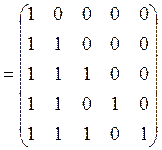Поскольку , отношение  не является транзитивным.

Итак, отношение  обладает свойствами рефлексивности и антисимметричности.

Задача 17. Заданы множества  и . Запишите все функциональные соответствия на множестве   с помощью двустрочных матриц и матриц инциденций. Укажите, какие из них являются инъективными, сюръективными, взаимно однозначными.

Решение.

Составим все возможные двустрочные матрицы, в которых первая строка – последовательность элементов множества , вторая их образы во множестве . Для каждой двустрочной матрицы запишем соответствующую матрицу инциденций.

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; .

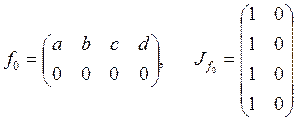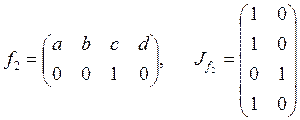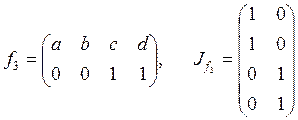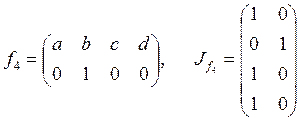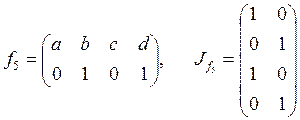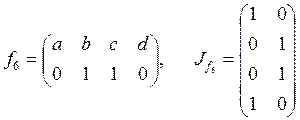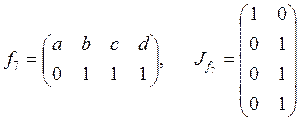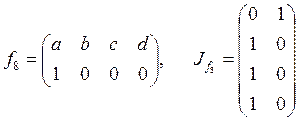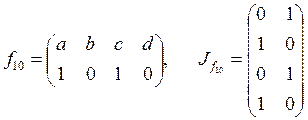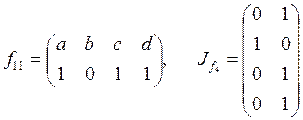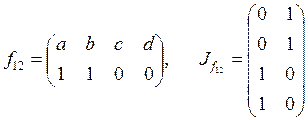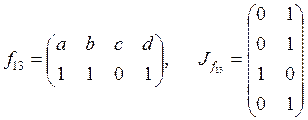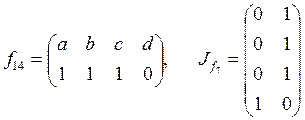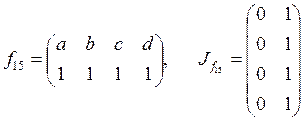На множестве  существует 2⁴=16 различных функциональных соответствий. Инъективных и взаимно однозначных соответствий среди них нет, так как  число элементов множества  меньше числа элементов множества .

Соответствия  являются сюръективными, поскольку каждый элемент множества  имеет в этих соответствиях не менее одного прообраза.

Соответствия  и  не относятся ни к какому виду соответствий. поскольку некоторые элементы множества  имеют в этих соответствиях более одного прообраза, а другие – ни одного прообраза.

Задача 18. В условиях задачи 17 запишите все функциональные соответствия  на множестве . Выделите среди них инъективные, сюръективные и взаимно однозначные.

Решение.

Составим все возможные двустрочные матрицы, в которых первая строка – последовательность элементов множества , вторая – их образы во множестве . Для каждой двустрочной матрицы запишем соответствующую матрицу инциденций.

Двустрочные матрицы будем составлять  по следующему правилу. Выберем образ нуля. Для выбранного образа нуля выберем образ единицы.

Поскольку образом единицы может быть любой из четырех элементов множества , то при каждом фиксированном образе элемента нуль, будем получать четыре различных соответствия. Образом нуля также может быть любой из четырех элементов множества  . Следовательно, существует 44=16 различных функциональных соответствий на множестве .

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; .

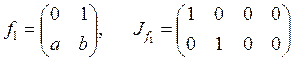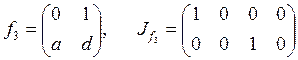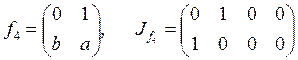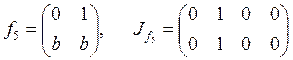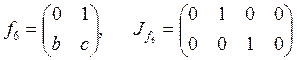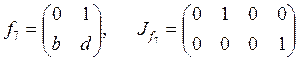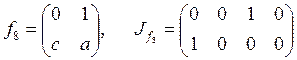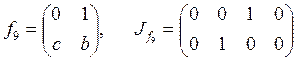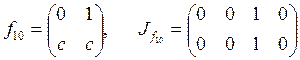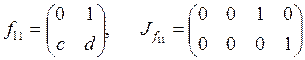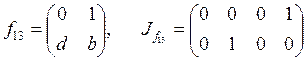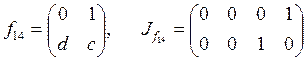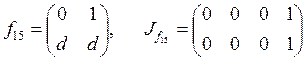Среди функциональных соответствий на множестве  не может быть сюръективных и взаимно однозначных, так как  число элементов множества  больше числа элементов множества .

Соответствия , ,  и  не относятся ни к какому виду соответствий, поскольку некоторые элементы множества  имеют в этих соответствиях более одного прообраза, а другие – ни одного прообраза.

Остальные 12 соответствий являются инъективными, так как каждый элемент множества  имеет в них не более одного прообраза.

Задача 19.  Даны множества , . На множестве  задано функциональное соответствие , график которого имеет вид: . Требуется:

1. Записать графики и матрицы инциденций отношений , , .

2. Записать графики отношений  и .

Решение.

1. а)  есть дополнение множества  до декартова произведения множеств .

Следовательно,  .

Запишем матрицы инциденций отношений  и :

,  .

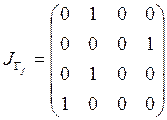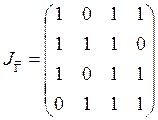б) Отношения  и  есть отношении на множестве .

Чтобы получить , надо в графике  поменять местами элементы во всех парах:

.

Матрица инциденций отношения :

.

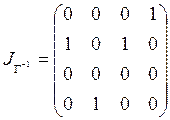Примечание 1. Обратим внимание на то, что .

Примечание 2. Отношение  не является функциональным соответствием на множестве , поскольку элемент  имеет два образа  и  ().

в)  есть дополнение множества  до декартова произведения множеств :

;

Матрица инциденций отношения :

.

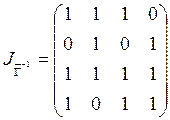2. Найдем композиции отношений  и .

Отношения  и  есть отношения на множестве .

;

;

;

.

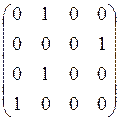
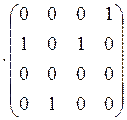
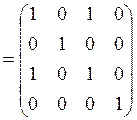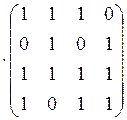
Примечание 3. Обратим внимание на то, что  есть дополнение отношения  до множества .