Вариант 7
1. Представить
множества 
, 
,
, 
на
диаграмме Эйлера-Венна. Записать характеристические функции множеств 
, 
и
в виде двоичных векторов.
Пронумеровать каждую область диаграммы Эйлера-Венна двоичным номером.
2. Доказать равенства: 
,
где 
и 
–
подмножества какого-либо универсального множества 
.
3. Бинарные отношения 
и
на множестве 
заданы
характеристическими свойствами 
, 
.
Требуется:
1) записать матрицы инциденций этих отношений,
2) найти композиции 
и 
,
3) проиллюстрировать решение с помощью графов.
4. На множестве задано
бинарное отношение: 
. Определите, является ли
данное отношение транзитивным. Укажите опосредованные связи между элементами множества
в отношении 
.
5. В спортивном празднике участвовали 120 студентов. На празднике студенты выступали в трех видах соревнований художественная гимнастика (вид Г), легкая атлетика (вид А) и боевые единоборства (вид Б). В виде Г участвовали 70 студентов, в А – 50 студентов, в Б – 30, в Г и А – 15, в Г и Б – 15, в А и Б – 10. Сколько студентов участвовали во всех трех видах соревнований?
6. Сколькими способами можно распределить 5 подарков между 1) четырьмя, 2) тремя, 3) пятью детьми?
7. Докажите, что импликации не коммутативная операция, а конъюнкция не дистрибутивна относительно импликации.
8. Запишите
функцию 
, используя
1) операции кольцевая сумма и конъюнкция, 2) операции импликация, конъюнкция и отрицание.
9. Дано высказывание :
"Если Земля вращается вокруг Солнца, а Луна – вокруг Земли, то Солнце
вращается вокруг Луны". Требуется:
1)
Выделить в высказывании атомарные
высказывания,
2)
Представить в виде формулы логики высказываний с
использованием импликации,
3)
Составить таблицу истинности высказывания ,
4) Представить в
виде формулы логики высказываний без импликации.
10. Даны формулы алгебры высказываний: 
, 
,
.
Найти среди них тавтологии и тождественно ложные формулы.
11. Граф 
задан
матрицей инциденций:
.
.
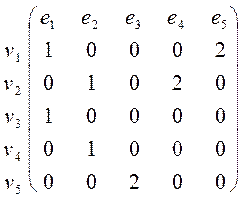Требуется:
1) построить граф ;
2) найти степень каждой из его вершин;
3) записать матрицу смежности графа;
4) записать список ребер графа.
12. Ориентированный граф задан матрицей инциденций:
.
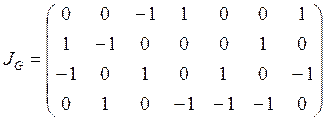Требуется:
1) построить граф;
2) построить какой-либо остов и соответствующий ему коостов графа;
3) записать матрицу базисных циклов и матрицу базисных разрезов графа;
4) проверить ортогональность пространства базисных циклов пространству базисных разрезов графа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
