Определим вид расстановок.
Для этого ответим на вопросы схемы определения вида расстановок.
а) Расстановки отличаются составом элементов (например, (1,1,3,2), (4,1,3,2)). Расстановки являются размещениями или сочетаниями.
б) Расстановки отличаются порядком элементов (например, (1,1,3,2) и (3,1,2,1)). Расстановки являются размещениями.
в) Элементы в расстановках повторяются. Расстановки есть размещения с повторениями из четырех элементов по четыре элемента.
Число таких размещений 
.
Очевидно, что если обитателей трое или пятеро, то речь идет о размещениях с повторениями из четырех элементов по три элемента и по пять элементов соответственно.
Следовательно,
– число способов
расселить трех человек по четырем комнатам,
– число способов
расселить пять жильцов по четырем комнатам.
Задача 24.
Пусть 
– квадратная пластинка, вставленная
в нишу в стене. Углы ниши помечены номерами 1, 2, 3, 4. Сколько существует
способов расположения пластинки в нише, если 1) пластинку можно поворачивать вокруг
центра симметрии, 2) пластинку можно зеркально отражать от осей симметрии квадрата?
Решение.
Для удобства пронумеруем углы пластинки также номерами 1,2,3,4.
 |
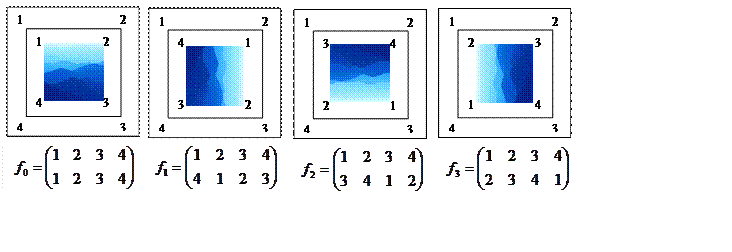Как видно из рисунка, поворот пластинки вокруг центра
симметрии квадрата дает четыре различные подстановки, среди которых 
– тождественная подстановка.
 |
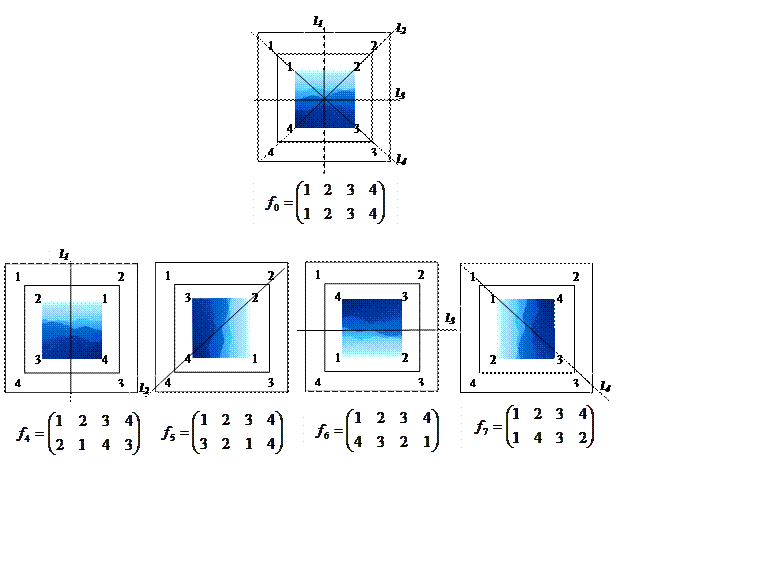Ответ:
существует 8 подстановок связанных с поворотом квадрата вокруг его центра
симметрии и отражением от осей симметрии, среди которых тождественная
подстановка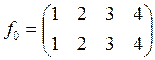 
.
Задача 25. Пусть – 
– подстановки, связанные с
преобразованиями симметрии квадрата (см. задачу 24). Требуется:
1) найти, число всех подстановок из четырех элементов;
2) выполнить а) композиции подстановки 
с подстановками 
, 
, 
; б) композиции подстановки 
с подстановками , 
, (задача 24).
Решение.
1) Число различных подстановок из четырех элементов равно числу перестановок без повторений из четырех элементов.
Следовательно, число всех подстановок равно 
.
2) Выпишем подстановки –
и выполним нужные композиции.
, 
,
, 
,
, 
.
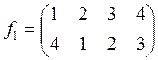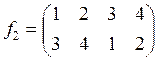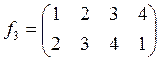
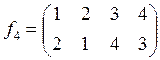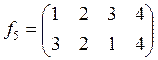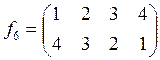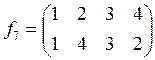а)
;
;
.
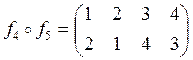
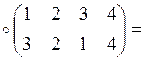
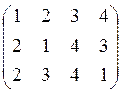
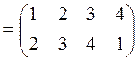
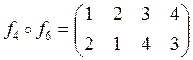
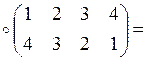
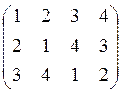
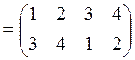
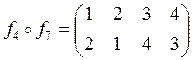
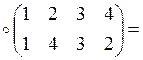
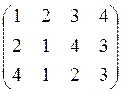
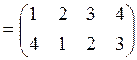
б)
;
;
.
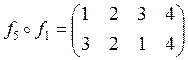
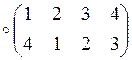
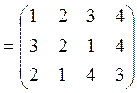
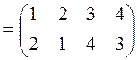
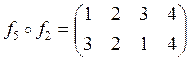
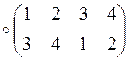
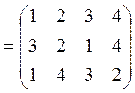
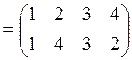
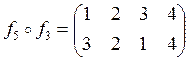
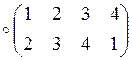
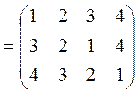
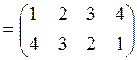
Задача 26.
Имеются метки трех типов 
, 
и 
.
Сколькими способами можно пометить этими метками семь объектов так, чтобы было
использовано по три метки типов и и одна метка типа ?
Решение.
Запишем несколько результатов операции расстановки меток в виде двустрочных матриц:
, 
, 
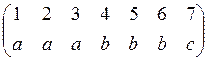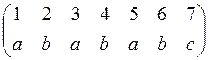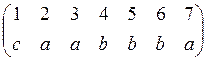и
т.п.
Определим вид расстановок, для чего ответим на вопросы схемы определения вида расстановок.
а) Расстановки не отличаются составом элементов. Расстановки являются перестановками.
б) Элементы в расстановках повторяются. Расстановки есть перестановками с повторениями из трех элементов по семь элементов.
Число таких перестановок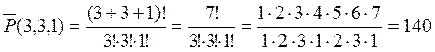 
.
Задача 27. На слет туристов едет команда в 7 человек. Туризмом в университете занимаются 10 юношей и 8 девушек. Сколько существует способов составить команду на слет 1) из одних юношей, 2) из одних девушек 3) из четырех юношей и трех девушек?
Решение.
1) Определим вид расстановок при составлении команды из юношей.
а) Расстановки отличаются составом элементов (например, (А,Б,С,Д,Е,И,К) и (Ю,А,Б,С,Д,Е,И)). Расстановки являются размещениями или сочетаниями.
б) Расстановки не отличаются порядком элементов (например, (А,Б,С,Д,Е,И,К) и (К,Б,С,Д,Е,И,А) – состав одной и той же команды). Расстановки являются сочетаниями.
в) Элементы в расстановках не повторяются. Расстановки есть сочетания без повторений из 10 элементов по 7 элементов.
Число таких сочетаний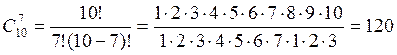 
.
2) Аналогично число способов составить команду из одних девушек равно числу сочетаний без повторений из 8 элементов по 7 элементов:
.
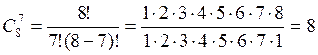3) Число способов выбрать в команду четырех юношей равно числу сочетаний без повторений из 10 элементов по 4 элемента:
.
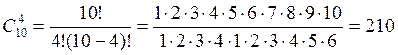Число способов выбрать в команду трех девушек равно числу сочетаний без повторений из 8 элементов по 3 элемента:
.
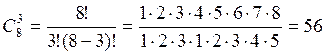Команда из четырех юношей и трех девушек представляет собой пару ((4Ю),(3Д)). Число способов выбрать первый элемент в этой паре равно 210, второй – 56. Согласно правилу произведения, существует 210·56 = 1680 пар такого рода.
Ответ. Существует 120 способов составить команду из одних юношей, 210 – из одних девушек, 1680 – из четырех юношей и трех девушек?
Задача 28. Молодой человек, отправляясь на свидание с девушкой, купил пять коробок конфет. Сколькими способами может девушка распределить этот подарок между собой и щедрым юношей, если 1) все коробки были одинаковыми, 2) все коробки разные, 3) имелось 3 коробки одного вида и 2 коробки другого вида?
Решение.
Пусть {Д,Ю} – множество людей, между которыми надо распределить коробки, {1,2,3,4,5}- множество коробок конфет.
1) Составим несколько вариантов распределения подарка, при условии, что коробки одинаковые:
, 
, 
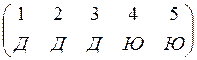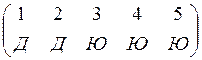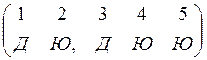и
т.п.
Определим вид расстановок.
а) Расстановки отличаются составом элементов ( например, (Д,Д,Д,Ю,Ю) – три коробки девушке, две – юноше, (Д,Д,Ю,Ю,Ю) – две девушке, три юноше). Расстановки являются размещениями или сочетаниями.
б) Поскольку все коробки конфет одинаковы, расстановки порядком элементов не отличаются, (например, (Д,Д,Ю,Ю,Ю) и (Д,Ю,Д,Ю,Ю) – один и тот же вариант распределения: две коробки девушке, три – юноше). Расстановки являются сочетаниями.
в) Элементы в расстановках могут повторяться. Расстановки есть сочетания с повторениями из 2 (юноша и девушка) элементов по 5 элементов (коробки крнфет).
.
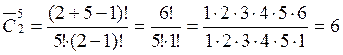2) Пусть все коробки разные. Варианты распределения коробок, рассмотренные в первом пункте, в этом случае получают другую интерпретацию.
а) Расстановки отличаются составом элементов ( например, (Д,Д,Д,Ю,Ю) – три первые коробки девушке, две последние – юноше, (Д,Д,Ю,Ю,Ю) – две первые девушке, три последние – юноше). Расстановки являются размещениями или сочетаниями.
б) Поскольку все коробки конфет разные, расстановки отличаются порядком элементов, (например, (Д,Д,Ю,Ю,Ю) и (Д,Ю,Д,Ю,Ю) различны, так как набор из первой и второй коробки, полученные девушкой отличается от набора из первой и третьей коробок). Расстановки являются размещениями.
в) Элементы в расстановках могут повторяться. Расстановки есть размещения с повторениями из двух элементов по пять элементов.
.
3) Для вычисления числа вариантов распределения при условии, что 3 коробки одного вида и 2 коробки другого вида, сначала распределим коробки одного вида, а затем другого.
Число способов распределить три одинаковые коробки между юношей и девушкой, по аналогии с первым пунктом задачи, есть число сочетаний с повторениями из 2 элементов по 3 элемента:
;
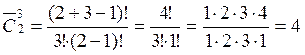число способов распределить две одинаковые коробки между юношей и девушкой есть число сочетаний с повторениями из 2 элементов по 2 элемента:
.
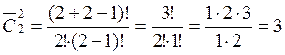Итак, число способов распределить коробки первого вида равно 4, второго – 3. Следовательно, число способов распределить оба вида коробок, согласно правилу произведения, равно 4·3=12
Задача 29. Проверьте вычислением, что 
.
Решение.
Применяя формулы вычисления числа сочетаний без повторений, имеем:
;
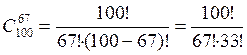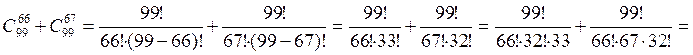
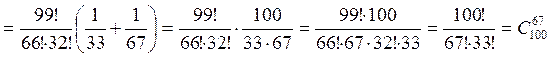, что и требовалось доказать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.