
Задача 1:
Составим математическую модель задачи. Пусть x1, х2 соответственно - количество единиц изделий, изготавливает предприятие. По смыслу задачи эти переменные неотрицательны.
Тогда F(x1, x2) = 2*x1 + 3*x2 - совокупная прибыль от продажи произведенной продукции.
Подсчитаем затраты времени:
1й станок: 10*х1 + 5*х2, по условию затраты не превосходят 10,
2й станок: 6*х1 + 10*х2 , по условию затраты не превосходят 10.
3й станок: 8*х1 + 15*х2 , по условию затраты не превосходят 10.
Пришли к задаче линейного программирования:
F(x1, x2) = 2*x1 + 3*x2 --> max,
x1 ≥ 0, x2 ≥ 0
10*х1 + 5*х2 ≤ 10
6*х1 + 10*х2 ≤ 10
8*х1 + 15*х2 ≤ 10
Теперь перейдем к канонической форме задачи, для решения ее симплекс-методом, для этого введем новые переменные x3, x4, x5 для перевода неравенства в равенство:
10*х1 + 5*х2 +x3 = 10
6*х1 + 10*х2 + x4 = 10
8*х1 + 15*х2 + x5 = 10
F(x1, x2) = 2*x1 + 3*x2 + 0*x3 + 0*x4 + 0*x5
Исходный опорный план:
приравниваем x1 = 0, x2 = 0
(x1, x2, x3, x4, x5) = (0, 0, 10, 10, 10)
Оптимальный план:
(x1, x2, x3, x4, x5) = (57, 12, 30, 0, 0)
x1 = 141 (изделие 1), x2 = 75 (изделие 2),
Максимальная прибыль
F = 2 * 421 + 3 * 298 = 1736
Ответ: На предприятии следует выпускать 421 единиц 1го изделия и 298 второго, для обеспечения оптимальных объемов производства.
Задача 2:
Составим математическую модель задачи. Пусть x1, х2 соответственно - количество единиц изделий, изготавливает предприятие. По смыслу задачи эти переменные неотрицательны.
Тогда F(x1, x2) = 40*x1 + 360*x2 - совокупная прибыль от продажи произведенной продукции.
Подсчитаем затраты кормов:
Затраты 1го корма: 10*х1 + 140*х2, по условию затраты не превосходят 64000,
Затраты 2го корма: 12*х1, по условию затраты не превосходят 9600.
Затраты 3го корма: 28*х1 + 48*х2 , по условию затраты не превосходят 41600.
Затраты 4го корма: 21*х1 + 12*х2 , по условию затраты не превосходят 21600.
Пришли к задаче линейного программирования:
F(x1, x2) = 40*x1 + 360*x2 --> max,
x1 ≥ 0, x2 ≥ 0
10*х1 + 140*х2 ≤ 64000
12*х1 ≤ 9600
28*х1 + 48*х2 ≤ 41600
21*х1 + 12*х2 ≤ 21600
Теперь перейдем к канонической форме задачи, для решения ее симплекс-методом, для этого введем новые переменные x3, x4, x5, x6 для перевода неравенства в равенство:
10*х1 + 140*х2 +x3 = 64000
12*х1 + x4 = 9600
28*х1 + 48*х2 + x5 = 41600
21*х1 + 12*х2 + x6 = 21600
F(x1, x2) = 40*x1 + 360*x2 + 0*x3 + 0*x4 + 0*x5 + 0*x6
Исходный опорный план:
приравниваем x1 = 0, x2 = 0
(x1, x2, x3, x4, x5, x6) = (0, 0, 64000, 9600, 41600, 21600)
Оптимальный план:
(x1, x2, x3, x4, x5) = (657, 248, 76,0, 0, 0)
x1 = 657 (коровы), x2 = 248 (свиньи),
x3 = 76 (корм 2 вида не используется на 76 единиц)
Максимальная прибыль
F = 40 * 657 + 360 * 248 = 115560.
Ответ: На звероферме следует выпускать 657 коров и 248 свиней.
Задача 3:
Построим опорный план и найдем минимальный элемент матрицы стоимостей:
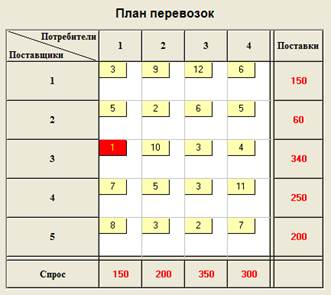
Запас 3-го поставщика больше спроса 1-го потребителя. Полагаем элемент матрицы плана равным спросу 1-го потребителя, уменьшаем запас 3-го поставщика на величину спроса 1-го потребителя и исключаем 1-й столбец из дальнейшего поиска.
Среди потребителей, спросы которых не удовлетворены, и среди поставщиков, запасы которых не исчерпаны, ищем минимальный элемент матрицы стоимостей.
Спрос 2-го потребителя больше запаса 2-го поставщика. Полагаем элемент матрицы плана равным запасу 2-го поставщика уменьшаем спрос 2-го потребителя на величину запаса 2-го поставщика и исключаем 2-ю строку из дальнейшего поиска.
Cреди поставщиков, запасы которых не исчерпаны, и среди потребителей, спрос которых не удовлетворен, ищем минимальный элемент матрицы стоимостей.
Запас 5-го поставщика не больше спроса 3-го потребителя. Полагаем элемент матрицы плана равным запасу 5-го поставщика, уменьшаем спрос 3-го потребителя на величину запаса 5-го поставщика и исключаем 5-ю строку из дальнейшего поиска.
Среди потребителей, спросы которых не удовлетворены, и среди поставщиков, запасы которых не исчерпаны, ищем минимальный элемент матрицы стоимостей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.