Статистические наблюдения. Способ учета фактов во времени. Несплошные виды наблюдений

открытых  интервалов (первого  и  последнего)  условно  приравниваются  к  величинам интервалов, примыкающих к ним (второго и предпоследнего). С учетом этого середины интервалов будут следующими:

23; 25; 27; 29; 31; 33

Используя  среднюю  арифметическую  взвешенную,  определим средневзвешенное время, необходимое для изготовления одной детали:

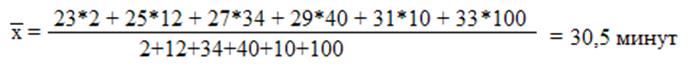
Находим дисперсию:

s²= ((23-30,5)*2 +(25-30,5)*12 +(27-30,5)*34 +(29-30,5)*40 +(31-30,5)*10 +

+(33-30,5)*100)/198 = 5

Т.к. величина среднего математического отклонения, это есть величина корня квадратного из дисперсии, то находим его:

s=√s² = 2,24 мин.

Ответ: среднее математическое отклонение составило 2,24 мин.

          Задача 8.25. Для установления среднего возраста читателей библиотеки намечено провести выборочное наблюдение методом механического отбора данных из читательских карточек (всего читателей в библиотеке – 50 тыс. человек). Предварительно установлено, что среднее квадратическое отклонение возраста читателей равно 10 годам.

Требуется определить необходимую численность выборки при условии, что с вероятностью 0,95 ошибка выборки будет не более 2 лет.

Решение:

Для решения задачи нам необходимо использовать следующую формулу:

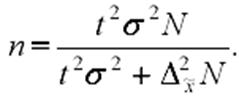
Где n – искомая численность выборки

s² – квадрат среднего математического ожидания (дисперсия),

t – параметр зависящий от уровня вероятности p

По условию задачи, уровень вероятности составляет 0,95, для определения параметра t, необходимо воспользоваться следующей таблицей:

Кроме того по условию заданы следующие параметры:

N=50000

s=10

D²_x = 2

Подставляем в формулу наши, заданные значения:

n= 1,96² *10² *50000 / (1,96² *10² + 2² *50000) = 95,86 » 96

С  учетом  полученного  необходимого  объема  выборки (96 читателей)  определим  интервал  отбора: 50000:96=520,83.

Определенный таким способом интервал всегда округляется в меньшую сторону,  так  как  при  округлении  в  большую  сторону  произведенная выборка не достигнет рассчитанного по формуле необходимого объема.

Следовательно,  в  нашем  примере,  из  общего  списка  читалей библиотеки необходимо отобрать для обследования каждого 520-го человека.

При этом процент отбора составит 0,19% (100%:520).  

Ответ: необходимо, для обследования, отбирать данные каждого 520-го человека.

Задача 9.8. Имеются следующие данные о вводе в действие жилых домов по Кемеровской области (тысяч квадратных метров общей площади):

На основе приведенных данных вычислите:

1)  средний уровень ряда;

2)  цепные и базисные темпы роста;

3)  средний абсолютный прирост.

Решение:

1) Средний уровень ряда (y), для  интервальных  равноотстоящих  рядов, находится по формуле простой средней арифметической:

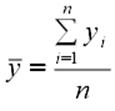
y = 679,34

2) Цепные и базисные темпы роста:

Цепной темп роста будет равен: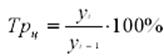

Базисный темп роста: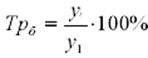

Цепной темп роста:	Базисный темп роста:
y2= (781,2/855)* 100% = 91,4 %	y2= (781,2/855)* 100% = 91,4 %
y3= (563,1/781,2)*100% = 72,1%	y3= (563,1/855)*100% = 65,9%
y4= (650,4/563,1)*100% = 115,5%	y4= (650,4/855)*100% = 76,1%
y5= (547/650,4)*100% = 84,1%	y5= (547/855)*100% = 64,0%

Вывод: исходя из полученных данных, мы видим, что темпы роста снижаются, в каждом новом году, становясь меньше, чем в предыдущем, и почти в 2 раза меньше по итогам последнего года.

3) Средний абсолютный прирост

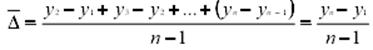
D= -77

Вывод: значение среднего абсолютного прироста получилось отрицательное, это говорит, что эта величина в данном примере не прирост, а уменьшение.

Задача 10.8. Имеются следующие данные о стоимости реализованной продукции по совхозу за два года (базисный и отчетный): 

Виды продукции	Стоимость продукции, млн руб.		Повышение средних цен реализации в отчетном году по сравнению с базисным, %
	базисный год	отчетный год
Мясо КРС	70	75	+25
Мясо свиней	50	70	+27
Молоко	190	300	+14

1.  Используя индексный метод, вычислите изменение стоимостного объема реализованной продукции (выручки) в отчетном году по сравнению с базисным за счет изменения физического объема продукции и средних цен реализации.

2.  На основании полученных данных сделайте краткие выводы.

Решение:

1) С учетом приростов средних цен реализации несложно определить, что значения индексов в отчетном году будут составлять