Спрос 3-го потребителя не больше запаса 3-го поставщика. Полагаем элемент матрицы плана равным спросу 3-го потребителя, уменьшаем запас 3-го поставщика на величину спроса 3-го потребителя и исключаем 3-й столбец из дальнейшего поиска.
Cреди поставщиков, запасы которых не исчерпаны, и среди потребителей, спрос которых не удовлетворен, ищем минимальный элемент матрицы стоимостей.
Запас 3-го поставщика не больше спроса 4-го потребителя. Полагаем элемент матрицы плана равным запасу 3-го поставщика, уменьшаем спрос 4-го потребителя на величину запаса 3-го поставщика и исключаем 3-ю строку из дальнейшего поиска.
Среди потребителей, спросы которых не удовлетворены, и среди поставщиков, запасы которых не исчерпаны, ищем минимальный элемент матрицы стоимостей.
Спрос 2-го потребителя не больше запаса 4-го поставщика. Полагаем элемент матрицы плана равным спросу 2-го потребителя, уменьшаем запас 4-го поставщика на величину спроса 2-го потребителя и исключаем 2-й столбец из дальнейшего поиска.
Cреди поставщиков, запасы которых не исчерпаны, и среди потребителей, спрос которых не удовлетворен, ищем минимальный элемент матрицы стоимостей.
Запас 1-го поставщика не больше спроса 4-го потребителя. Полагаем элемент матрицы плана равным запасу 1-го поставщика, уменьшаем спрос 4-го потребителя на величину запаса 1-го поставщика и исключаем 1-ю строку из дальнейшего поиска.
Среди потребителей, спросы которых не удовлетворены, и среди поставщиков, запасы которых не исчерпаны, ищем минимальный элемент матрицы стоимостей.
Спрос 4-го потребителя не больше запаса 4-го поставщика. Полагаем элемент матрицы плана равным спросу 4-го потребителя, уменьшаем запас 4-го поставщика на величину спроса 4-го потребителя и исключаем 4-й столбец из дальнейшего поиска.
Исходный опорный план построен:

Общие затраты на перевозку S = 4090
Для проверки опорного плана на оптимальность вычислим характеристики (маргинальные затраты) всех свободных клеток. Определение характеристик будем производить методом потенциалов.
Ищем первую строку, потенциал которой не определен.
Это строка с номером 1. Потенциал этой строки выбирается произвольно. Положим его равным нулю.
Остальные потенциалы определяются из условия, что в клетке, где записана базисная перевозка, p_i + q_j = c_ij. Последовательно определяем потенциал 4-го столбца, потенциал 3-й строки, потенциал 4-й строки, потенциал 1-го столбца, потенциал 3-го столбца, потенциал 2-го столбца, потенциал 2-й строки, потенциал 5-й строки.
Ищем первую строку, потенциал которой не определен.
Потенциалы всех строк и столбцов определены:
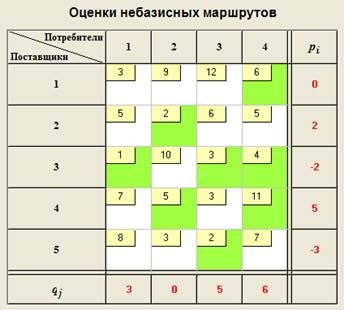
Характеристики клеток таблицы определяем по формуле, w_ij = c_ij - (p_i + q_j). Ясно, что для базовых клеток характеристики равны нулю. Вычислим характеристики w_ij для небазовых клеток и впишем в свободные клетки таблицы.
Среди характеристик небазовых клеток есть отрицательные. Для улучшения плана надо заполнить одну из этих клеток. Найдем клетку с наименьшим значением характеристики.
Это клетка на пересечении 4-й строки и 3-го столбца.
Добавим в план перевозку (4,3). При этом план перевозок должен оставаться планом (суммы по строкам и столбцам менять нельзя) и при том планом опорным: добавив одну базовую перевозку, нужно одну исключить, чтобы их общее число не изменилось. Найдем цепочку элементов, изменяемых при включении в базисное решение нового элемента.
Цепочка изменяемых базисных элементов должна начинаться с базисной перевозки, находящейся в 4-ой строке и заканчиваться базисной перевозкой, стоящей в 3-м столбце. При этом значение новой базисной переменной будет вычитаться из нечетных элементов цепочки и добавляться к четным элементам цепочки.
Получим новый опорный план перевозок:
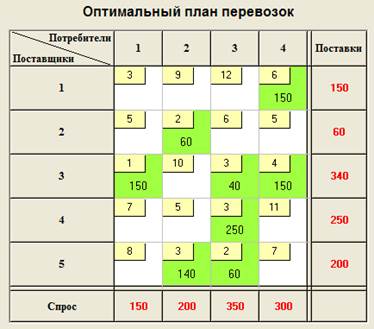
Общие затраты на перевозку S = 3180
Ответ:
Оптимальным будет следующий план:
0 0 0 150
0 60 0 0
Xопт = 150 0 40 150
0 0 250 0
0 140 60 0
При этом минимальные затраты не перевозку составят 3180.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.