Выбор параметров А и В зависит от вида корреляционной функции, характеризующей взаимосвязь между отдельными значениями случайного процесса.
Будем формировать случайный сигнал, отвечающий корреляционной функции вида:
![]() (3.2)
(3.2)
где: ![]() –
корреляционная функция,
–
корреляционная функция,
![]() – дисперсия,
– дисперсия,
α – коэффициент корреляции.
В случае корреляционной функции вида (3.2) коэффициенты A1 и B вычисляются по следующим формулам:
![]()
![]()
Стандартную величину Z, распределенную по нормальному закону с нулевым математическим ожиданием и единичной дисперсией будем вычислять по следующей формуле:
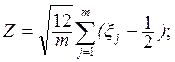 (3.3)
(3.3)
где ![]() –
случайные величины с равномерным на интервале [0, 1] распределением;
–
случайные величины с равномерным на интервале [0, 1] распределением;
m – некоторое натуральное число.
При машинной реализации
модели величины ![]() будем получать, используя
стандартную функцию языка «СИ».
будем получать, используя
стандартную функцию языка «СИ».
Для получения величины Z, распределенной по нормальному закону, значения m должны удовлетворять условию m>10.
Возьмем, для удобства, m=12. Тогда величину Zбудем вычислять по более простой, чем (3.3), формуле:
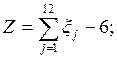 (3.4)
(3.4)
Получив на основании приведенных выше формул центрированные значения случайного процесса, можно легко перейти к нецентрированным значениям, используя следующую формулу:
![]()
где МХ – математическое ожидание случайной величины X.
4. Задание численных значений параметров.
Зададим вначале группу параметров, отвечающих конструктивным особенностям элементов системы, сохраняя принятые ранее обозначения.
Таблица 1.
|
Параметр |
Значение |
Единица измерения |
|
y0 |
100 |
кг/м³ |
|
ρ |
500 |
кг/м³ |
|
V |
1 |
м³ |
|
ω20 |
100 |
с-1 |
|
a1 |
10-5 |
м³ |
|
a2 |
2∙10-6 |
м³ |
|
КД |
0,01 |
В-м³/кг |
|
ТИ |
5 |
c |
|
КИ |
1 |
1/В-с |
Теперь зададим временные параметры системы.
Интервал времени ∆t выберем, исходя из следующего предположения: интервал времени ∆t должен быть в 10 раз меньше минимальной постоянной времени. Последняя в данном случае есть постоянная времени исполнительного механизма, и равна она 5. Следовательно, выберем:
∆t = 0,5 с.
Тогда при выборке в 3000 точек время моделирования составит:
3000 ∙ 0,5 = 1500 с.
Начальное значение возмущающего воздействия положим равным его математическому ожиданию:
X(t0) = MX;
Следующая группа параметров включает коэффициент настройки регулятора и характеристики случайного процесса.
Таблица 2.
|
Параметр |
Значение |
Единица измерения |
|
KР |
900 |
- |
|
MX |
0,0012 |
1/с |
|
σХ |
0,00008 |
1/с |
|
α |
0,022 |
1/с |
Разработку машинной программы моделирования будем проводить, используя инструментальную систему «Турбо СИ».
Полный текст программы со всеми необходимыми комментариями будет приведен ниже, в п.6; здесь же отметим некоторые особенности разрабатываемой программы.
Как указывалось выше, программа должна иметь графический пользовательский интерфейс с отображением на экране трендов параметров и выводом величин, характеризующих качество управления.
Однако в первую очередь ЭВМ должна решать дифференциальные уравнения системы численным методом, поэтому прокомментируем подробнее соответствующую часть программы.
Решение системы дифференциальных уравнений на ЭВМ производится с помощью явного метода Эйлера, согласно которому производная заменяется на конечное приращение.
В соответствии с этим, перепишем уравнения (2.12) и (2.13):
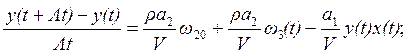 (5.1)
(5.1)
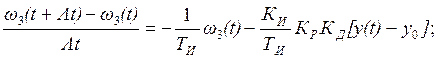 (5.2)
(5.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.