Моделирование системы регулирования концентрации в процессе мерсеризации, страница 3

Исполнительный механизм, вообще говоря, представляет собой совокупность исполнительного двигателя и дифференциала.

Однако поскольку дифференциал осуществляет функцию механического сложения оборотов основного двигателя и исполнительного, а частота вращения основного двигателя (ω₂₀) уже была учтена при выводе уравнения объекта, то при выводе уравнения исполнительного механизма будем рассматривать только исполнительный двигатель без дифференциала, а под самим исполнительным механизмом будем понимать только исполнительный двигатель.

На вход исполнительного механизма поступает сигнал с регулятора (напряжение U_р); на выходе его имеем регулирующее воздействие (ω₃). Таким образом, уравнение исполнительного механизма должно отражать связь между этими величинами.

Исполнительный механизм представляет собой двигатель постоянного тока с управлением со стороны цепи якоря (обмотки управления).

Электрическая схема двигателя представлена на рис.3:

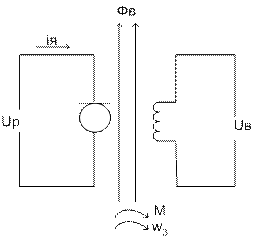
Рис.3. Электрическая схема двигателя.

На схеме использованы следующие обозначения:

i_я – ток якоря;

U_р – напряжение на выходе регулятора;

U_в – напряжение на обмотке возбуждения;

Ф_в – поток возбуждения;

М – вращающий момент;

ω₃ – частота вращения двигателя;

Для вывода уравнения исполнительного механизма воспользуемся далее некоторыми сведениями из курса электротехники.

Вращающий момент (М) двигателя определяется по следующей формуле:

М = С_мФ_вi_я;                                (2.5)

где С_м – постоянная двигателя, имеющая смысл его механической характеристики (безразмерная величина).

При изменении частоты вращения двигателя в цепи якоря возникает противо-ЭДС (Е_п), определяемая по следующей формуле:

Е_п = С_еФ_вi_я;                                        (2.6)

Согласно закону Кирхгофа:

U_р = i_яR_я + Е_п;   (2.7)

где R_я– активное сопротивление цепи якоря.

Подставим выражения для i_яиз формулы (2.7) в (2.5):

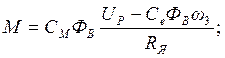                        (2.8)

Из курса механики известно уравнение Ньютона для вращательного движения:

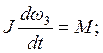   (2.9)

Подставив выражение для М из (2.8) в (2.9) и проведя несложные преобразования, получим:

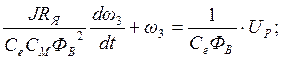              (2.10)

Введем новые обозначения:

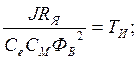
где T_и – постоянная времени исполнительного механизма;

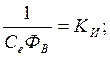
где К_и – коэффициент усиления исполнительного механизма.

Исходя из необходимости дальнейшего численного интегрирования на ЭВМ, перепишем уравнение (2.10) в следующем виде:

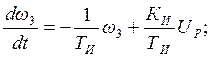                         (2.11)

Уравнение (2.11) и является уравнением исполнительного механизма.

Итак, получены математические модели элементов системы: уравнения (2.1), (2.3), (2.4), (2.11).

Запишем их еще раз:

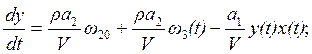
U_д(t)– U₀ = K_д[y(t)–y₀];

U_р = – K_р(U_д – U₀);

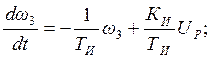
Видим, что в 4-х уравнениях присутствуют 5 неизвестных: y(t), x(t), ω₃(t),            (U_д(t)– U₀), U_р.

Однако, в силу взаимосвязи переменных между собой, можно сократить количество уравнений, исключив из них неизвестные: (U_д(t)– U₀) и U_р.

Проделав элементарные преобразования, получим систему 2-х дифференциальных уравнений с 3-мя неизвестными:

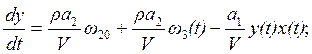         (2.12)

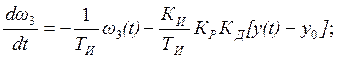     (2.13)

Полученная система уравнений является, по сути, математической моделью системы регулирования. Иными словами, получены уравнения, отражающие взаимосвязь регулируемой величины, регулирующего воздействия и возмущающего воздействия.

3. Формирование сигнала возмущающего воздействия.

Возмущающее воздействие будем формировать по определенному алгоритму как некоторый случайный сигнал.

Алгоритм формирования можно представить в виде следующей формулы:

                     (3.1)

где:  – центрированный случайный сигнал;

t_i – i-тый момент времени;

t_i-1 – (i–1)-й момент времени;

A₁, B – коэффициенты;

Z – стандартная случайная величина с нормальным распределением, нулевым математическим ожиданием и единичной дисперсией.

Обозначим ∆t – интервал времени между отдельными значениями сигнала:

∆t = t_i – t_i-1;