Моделирование системы регулирования концентрации в процессе мерсеризации, страница 2

w₃ – переменная частота вращения исполнительного двигателя;

w₂₀ – переменная частота вращения основного мощного двигателя;                                                                                                           

2. Вывод уравнений системы.

2.1. Уравнение объекта.

Объект управления образуют в совокупности следующие элементы:                            бак-мерсеризатор, бачок-дозатор, насос, привод насоса, транспортер-питатель и основной двигатель.

Состояние объекта характеризуется следующими параметрами:

ω₁(t) = x(t) – частота вращения привода насоса подачи пульпы;

ω₂₀ – частота вращения основного мощного двигателя;

ω₂ (t) – частота вращения на выходе дифференциала;

ρ – плотность сухой целлюлозы, кг/м³;

y(t) – концентрация пульпы в баке-мерсеризаторе, кг/м³;

V– объем смеси в баке-мерсеризаторе, м³.

Введем предположение о том, что внутри бака-мерсеризатора имеет место идеальное перемешивание.

Получим уравнение объекта, связывающее регулируемую величину (концентрацию целлюлозы в баке), возмущающее воздействие (изменение частоты вращения привода насоса) и регулирующее воздействие (изменение частоты вращения исполнительного двигателя).

Аналитическое уравнение объекта будем получать, руководствуясь следующими двумя принципами:

1)  Принцип бесконечно-малых величин;

2)  Принцип материального баланса.

Рассмотрим малый интервал времени dt. За это время концентрация целлюлозы изменится на величину dy.

Запишем уравнение материального баланса, т.е. выразим приращение количества (массы) целлюлозы в баке за время dt (равное Vdt) через разность входящего и выходящего потоков:

где a₁, a₂ – коэффициенты пропорциональности, отражающие конструктивные особенности элементов объекта и имеющие смысл объемов (м³).

Разделим полученное уравнение на Vdt:

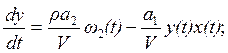
Для того чтобы полученное дифференциальное уравнение включало регулирующее воздействие [ω₃(t)] в явном виде, проведем преобразование, используя следующую формулу:

ω₂(t) = ω₂₀(t) + ω₃(t);

Тогда получим:

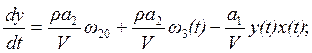                   (2.1)

Последнее дифференциальное уравнение и является уравнением объекта. Как видно, оно нелинейное, с нелинейностью типа произведения.

2.2. Уравнение датчика.

Конструктивно датчик концентрации представляет собой лопастную мешалку.

Принцип действия датчика состоит в следующем. Мешалка, вращаясь, испытывает некоторое сопротивление со стороны пульпы. Это сопротивление зависит от вязкости, которая, в свою очередь, является функцией концентрации целлюлозы. Измеренное таким образом значение концентрации преобразуется в электрический сигнал – напряжение.

Характеристика датчика изображена на рис. 2.

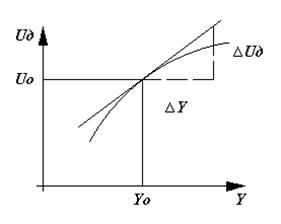
Рис.2. Характеристика датчика.

Сделаем некоторые предположения относительно свойств датчика:

1.  Инерционность датчика – мала (равна нулю).

2.  Зависимость выходного напряжения от концентрации – линейна.

Исходя из этого, запишем уравнение датчика:

U_д(t) = K_д[y(t)–y₀] + U₀;                     (2.2)

где U_д(t) – напряжение на выходе с датчика [В];

U₀– напряжение при номинальной (заданной) концентрации [В];

y₀ – номинальная концентрация [кг/м³];

y(t) – текущая концентрация [кг/м³];

K_д– коэффициент пропорциональности (передачи) [В-м³/кг];

Полученное уравнение можно преобразовать к равносильной форме, записанной в отклонениях:

U_д(t)– U₀ = K_д[y(t)–y₀];            (2.3)

2.3. Уравнение регулятора.

Как уже было сказано, регулятор реализует пропорциональный закон регулирования, формируя управляющий сигнал (напряжение) пропорционально ошибке регулирования, равной разности текущего и требуемого значения концентрации (либо соответствующих значений напряжения).

Запишем уравнение регулятора:

U_р = – K_р(U_д – U₀);                            (2.4)

где K_р – коэффициент передачи регулятора.

2.4. Уравнение исполнительного механизма.