Шпора по экзаменационым вопросам, страница 7

Эта работа совершается за счет энергии магнитного поля => 

Взаимная индукция

Рассмотрим два неподвижных контура.

Если в контуре 1 течёт ток I₁, то он создаёт в контуре 2 магнитный поток Ф_2,1=L_2,1*I₁

L_2,1 – коэффициент взаимной индуктивности.

Если ток I₁ переменный, то он вызовет в контуре 2 ЭДС:

Аналогично рассуждая можно сказать что ток I₂ текущий в контуре 2 вызовет в первом контуре ЭДС:

Это явление называется взаимной индукцией, причём L_1,2 = L_2,1

33.     Виды магнетиков.

Магнитный гистерезис.

Каждый атом это система кольцевых токов своеобразным движением по орбите. При движении электрона сила электрического тока равна: i=q/t=e/T=ev (T – период, v – частота вращения электрона)

Магнитный момент кольцевого тока электрона равен: P_m= i*S = e*D*S (S – площадь орбиты ). Следовательно каждый атом подобен витку с током и обладает магнитным моментом.

При отсутствии внешнего магнитного поля магнитные моменты атомов ориентированы хаотически. При внесении вещества в магнитное поле магнитные моменты атомов ориентируются. Вещество приобретённое магнитный момент – намагничивается. Магнитный момент единицы объёма вещества называется намагниченным

Возможны два случая:

1) Магнитные моменты атомов направлены против внешнего поля. Такие вещества ослабляют внешнее поле и называются диамагнетиками.

2) Магнитные моменты атомов ориентированы по направлению поля. Такие вещества усиливают магнитное поле и называются парамагнетиками.

Таким образом магнитное поле в веществе  складывается из внешнего   поля  и поля вещества: 

Величина называется магнитной проницаемостью вещества.

Для диамагнетиков μ<1, для парамагнетиков μ>1. Магнитное поле в веществе удобно описывать с помощью вспомогательной величины напряжённости магнитного поля Н.

Среди парамагнетиков есть вещество у которых μ достигает значений 10³ – 10⁴. Эти вещества называются ферромагнетиками.

Ферромагнетизм объясняется тем, что у этих веществ даже без внешнего поля существуют области спантаной намагниченности – домены. Домены легко ориентируются в магнитном поле. Кривая намагниченности ферромагнетиков имеет вид:

34.    Свободные электромагнитные колебания

в колебательном контуре.

Электромагнитные колебания называются периодическими изменениями заряда силы тока и напряжения в электрической цепи. Свободные электромагнитные колебания возможны в колебательном контуре цепи содержащий конденсатор и катешку.

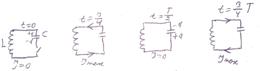
После полной разрядки конденсатора (рис 2) ток продолжает течь из за явления самоиндукции. И конденсатор перезаряжается (рис 3). Если пренебречь потенциальной энергией, то можно считать что заряд конденсатора остаётся неизменным.

По второму правилу Кирхгофа сумма напряжений в любом контуре равна ЭДС: U_c=E_сам

Следовательно:          - это дифференциальное уравнение гармонических колебаний.

Его решением будет функция q = q_max*sin ωt, где

Следовательно заряд в колебательном контуре изменяется по гармоническому закону с периодом  - формула Томсона.

Сила тока: I=q^’=q_max*ω cos ωt = I_max*cos ωt

Напряжение:

35.     Затухающие электромагнитные

колебания в колебательном контуре.

В реальном колебательном контуре сопротивлением пренебречь нельзя. В этом случае по второму правилу Кирхгофа сумма падений напряжения равна сумме ЭДС:

_{Обозначим:}

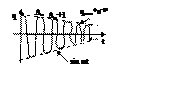
 Решением этого дифференциального уравнения будет функция:

график этой функции:

q_max*e^-βt – амплитуда затухающих колебаний

q_max – начальная амплитуда

β = R/2L – коэффициент затухания

  - частота затухания колебаний при R→0; ω→ω₀

Логарифмический декремент затухания:

Добротность колебательного контура:

Она показывает какая часть энергии теряется в контуре за 1 период.

36.     Вынужденные электромагнитные колебания.

Переменный электрический ток.

Переменный ток – это пример вынужденных колебаний в электрической цепи.

Пусть к электрической цепи приложено переменное напряжение:U=U_max*cos ωt, т.к. изменения напряжения и силы тока происходят медленно по сравнению со скоростью распространения электромагнитных взаимодействий, то значение напряжения и силы тока во всей цепи будут одинаковы. Такой ток называется квазистационарным. Для него выполняются законы Ома и Кирхгоффа.