Решение задач линейного программирования в соответствии с алгоритмом решения, так и с помощью пакета электронных таблиц Excel

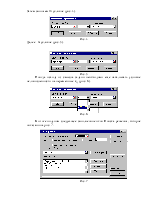
Цель работы: получение практических навыков решения задач линейного программирования в соответствии с алгоритмом решения, так и с помощью пакета электронных таблиц Excel.

Транспортная задача

Постановка задачи:

Имеется m пунктов отправления  A₁,A₂,…,A_m, которые обладают запасами однородного товара или груза в количестве  a₁,a₂,…,a_m соответственно. Имеется n пунктов назначения  B₁,B₂,…,B _n, которые подали заявки на b₁,b₂,…,b _n единиц товара соответственно. Пусть сумма всех запасов и сумма всех заявок равны, то есть .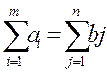

Известно C _ij – стоимость перевозки одного товара от каждого пункта отправления (ПО) A_i в каждый пункт назначения (ПН) B_j. Сформируем матрицу стоимости:

C=;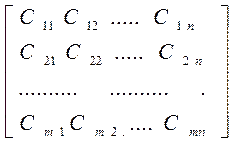

Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость перевозок была бы минимальна. Так как показателем эффективности является стоимость, то поставленная задача называться транспортной задачей (ТЗ) по критерию стоимости.

Математическая модель транспортной задача

Введем управляющую переменную x, пусть x_ij- количество груза, перевозимое из i-го ПО в j-ый ПН. Исходя из физического смысла задачи следует, что x_ij0 для всех i=, j=;

В транспортных задачах должны выполнятся следующие условия:

1.  суммарное количество груза, направленное из каждого ПО во все ПН должно быть равно запасу груза в данном пункте (так называемое m-условие), т.е. можно записать:

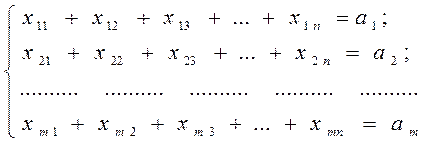
или

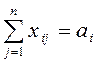
             .                                                             (1)

2.  суммарное количество груза, доставленное в каждый ПН из всех ПО должно быть равно заявке, поданной данным пунктом (так называемое n-условие).

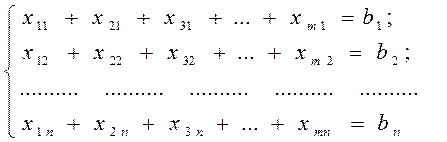
или в более компактном виде

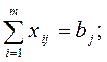
           .                                                               (2)

3.   суммарная стоимость всех перевозов должна быть минимальна.

L=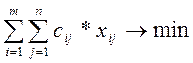                                                                       (3)

Целевая функция (3) и ограничения (1) и (2) являются линейными.

Особенности ТЗ

1.все коэффициенты при переменных (1) и (2) должны быть равны единице.

2.складывая между собой все уравнения (1) и (2) должны получить одно и тоже число в силу условия баланса:

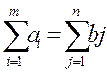.                                                                                         (4)

Таким образом, уравнения (1) и (2) связаны линейной зависимостью, и m+n-1 уравнения являются линейно независимыми. Эти уравнения можно разрешить относительно m+n-1 базисных переменных.  Количество свободных переменных обозначается через k=(m*n)-(m+n-1)=(m-1)(n-1). В ТЗ оптимальное решение достигается в одной из вершин ОДР, где, по крайней мере, k из переменных обращаются в ноль.

Основные определения и понятия ТЗ

Определение: значения x_ij называются перевозками.

Определение: любая совокупность x_ij называется планом перевозок.

Определение: план называется допустимым, если он удовлетворяет условиям (1) и (2), которые называются балансами условий, то есть все заявки удовлетворены и все запасы исчерпаны.

Определение: допустимый план называется опорным, если в нем отличных от нуля не более m+n-1 базисных перевозок, а остальные перевозки равны нулю.

Определение: план называется оптимальным, если он среди всех допустимых планов приводит к наименьшей стоимости всех перевозок.

При решении ТЗ манипулируем не симплексной таблицей, а транспортной, которая содержит:

1.  ПО и ПН;

2.  запасы, имеющиеся в ПО;

3.  заявки, поданные ПН;

4.  стоимость перевозок из каждого ПО в каждый ПН, которые помещены в правом верхнем углу ячейки.

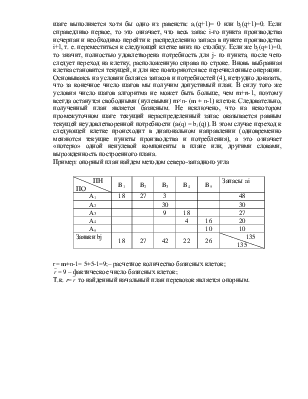
Общий вид транспортной таблицы приведен в табл. 1.

Таблица 1. Структура транспортной таблицы

Ячейки таблицы, в которых записаны отличные от нуля перевозки, называются базисными. Остальные ячейки называются свободными или пустыми.

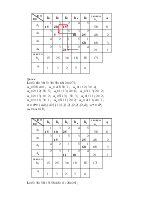
Построение исходного допустимого плана в транспортной задаче. Метод северо-западного угла

Решение транспортной задачи начинается с построения допустимого базисного плана. Наиболее простой способ его нахождения основывается на так называемом методе северо-западного угла. Суть метода состоит в последовательном распределении всех запасов, имеющихся в первом, втором и т. д. пунктах производства, по первому, второму и т. д.  пунктам потребления. Каждый шаг распределения сводится к попытке полного исчерпания запасов в очередном пункте производства или к попытке полного удовлетворения потребностей в очередном пункте потребления. На каждом шаге q величины текущих нераспределенных запасов обозначаются a_i(q), а текущих неудовлетворенных потребностей – b_j (q). Построение  допустимого начального плана начинается с левого верхнего угла (северо-западного угла) транспортной таблицы. При этом полагаем a_i(0)=a_i, b_j(0)=b_j. Для очередной клетки, расположенной в строке i и столбце j,  рассматриваются значения нераспределенного запаса в i-ом пункте производства и неудовлетворенной потребности j-ом пункте потребления. Из них выбирается минимальное и назначается в качестве объема перевозки между данными пунктами: x_ij=min{a_i(q), b_j(q)}. После этого значения нераспределенного запаса и неудовлетворенной потребности в соответствующих пунктах уменьшаются на данную величину: a_i(q+1)=a_i (q)–x_ij, b_j(q+1)=b_j(q)–x_ij Очевидно, что на каждом шаге выполняется хотя бы одно из равенств: a_i(q+1)= 0 или b_j(q+1)=0. Если справедливо первое, то это означает, что весь запас i-гo пункта производства исчерпан и необходимо перейти к распределению запаса в пункте производства i+l, т. е. переместиться к следующей клетке вниз по столбцу. Если же b_j(q+1)=0, то значит, полностью удовлетворена потребность для j- го пункта, после чего следует переход на клетку, расположенную справа по строке. Вновь выбранная клетка становится текущей, и для нее повторяются все перечисленные операции. Основываясь на условии баланса запасов и потребностей (4), нетрудно доказать, что за конечное число шагов мы получим допустимый план. В силу того же условия число шагов алгоритма не может быть больше, чем m+n-1, поэтому всегда останутся свободными (нулевыми) mn- (m + n-1) клеток. Следовательно, полученный план является базисным. Не исключено, что на некотором промежуточном шаге текущий нераспределенный запас оказывается равным текущей неудовлетворенной потребности (a_i(q) = b_j (q)). В этом случае переход к следующей клетке происходит в диагональном направлении (одновременно меняются текущие пункты производства и потребления), а это означает «потерю» одной ненулевой компоненты в плане или, другими словами, вырожденноcть построенного плана.