Решение задач линейного программирования в соответствии с алгоритмом решения, так и с помощью пакета электронных таблиц Excel, страница 3

Повторяя описанные выше действия найдем:

L=15+75+20+25+30+50+60+21=296;

=0+0-4= -4;  = -1+0-5= -6;  =1+3-3= 1;=3+3-1=5; 

=1+2-4= -1;   =3+2-2= 3;   =2+2-1= 3;   =0+2-5= -3; 

=1+(-1)-2= -2;   =3+(-1)-3= -1;   =0+(-1)-2= -3;   =-1+(-1)-4= -6;    

a^st = a²²= {2,2},{2,3},{1,3},{1,2};  a ^pq = a²³;

x_pq= x ₂₃= 5;

ПН ПО	B1	B2	B3	B4	B5		запасы     ai	ui
A1	1  15	3  20	2  15	4	5		50	0
A2	3	1  5	5	3  10	2  25		40	-2
A3	4	2	1	5	1  60		60	-3
A4	2	3	1  21	2	4		21	-1
заявки       bj	15	25	36	10	85		171
vj	1	3	2	5	4

Далее

L=15+60+30+5+30+50+60+21=271;

=5+0-4= 1;   = 4+0-5= -1;   =1+(-2)-3= -4;  

=2+(-2)-5= -5;   =1+(-3)-4= -6;   =3+(-3)-2= -2;  

=2+(-3)-1= -2;  =5+(-3) –5= -3;   =1+(-1)-2= -2;  

=3+(-1)-3= -1;   =5+(-1)-2= 2;   = 4+(-1)-4= -1;    

a^st = a⁴⁴= {4,4},{4,3},{1,3},{1,2},{2,2},{2,4};  a ^pq = a²⁴;

x_pq= x ₂₄= 10;

ПН ПО	B1	B2	B3	B4	B5	запасы     ai	ui
A1	1  15	3  10	2  25	4	5	50	0
A2	3	1   15	5	3	2  25	40	-2
A3	4	2	1	5	1  60	60	-3
A4	2	3	1  11	2  10	4	21	-1
заявки       bj	15	25	36	10	85	171
vj	1	3	2	3	4

L=15+30+50+15+50+60+11+20=251;

=3+0-4= -1;   = 4+0-5= -1;   =1+(-2)-3= -4;   =2+(-2)-5= -5;  

=3+(-2)-3= -2;   =1+(-3)-4= -6;   =3+(-3)-2= -2;   =2+(-3)-1= -2;  =3+(-3) –5= -3;   =1+(-1)-2= -2;   =3+(-1)-3= -1;   =5+(-1)-2= 2;  

= 4+(-1)-4= -1;    

Так как нет положительных оценок  - то получен оптимальный план записанным в последней транспортной таблице, при значении целевой функции L_min=251.

Решение транспортных задач с помощью электронных таблиц Excel

Транспортные задачи также легко решаются с помощью опции Поиск решения меню Сервис электронных таблиц Excel.

В качестве примера примем тот, который был рассмотрен выше.

Запишем исходные данные задачи в Excel (рис. 1) Здесь в ячейках B3:F6 записываются тарифы перевозок с_ij, а в ячейках B8:F11 начальные значения перевозок  принятых равными 1.

В ячейках J8:J11 запишем запасы ПО, а в ячейках B14:F14 заявки ПН.

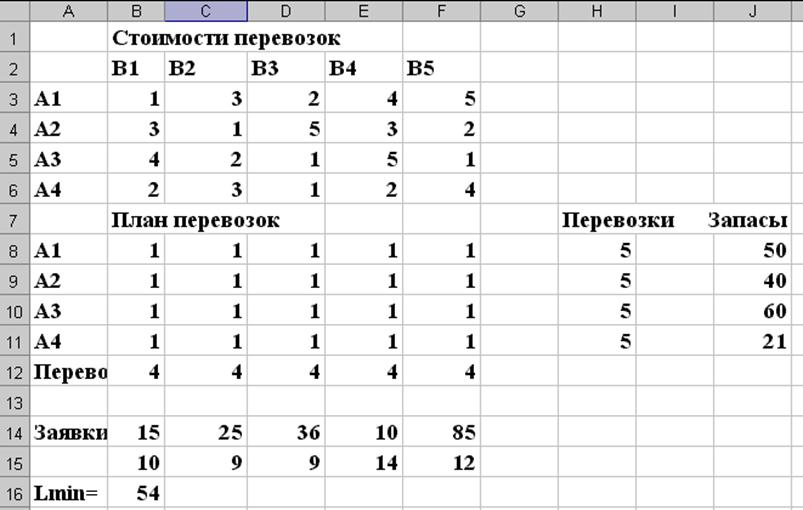
Рис. 1

Для выполнения m-условия подсчитаем количество перевозок, для каждого ПО А_i в ячейках H8:H11, как сумму значений в каждой строке. Для ячейки H8, это условие запишется в следующем виде =СУММ(B8:B11), аналогично для остальных (с учетом обозначения строк).

Для выполнения n-условия подсчитаем количество перевозок, для каждого ПH B_j в ячейках B12:F12, как сумму значений в каждом столбце. Для ячейки B12, это условие запишется в следующем виде =СУММ(B8:F8), аналогично для остальных (с учетом обозначения столбцов).

Целевая функция определяется, как сумма значений в ячейках B15:F15 (=СУММ(B15:F15)) и записывается в ячейку B16.

В ячейках B15:F15 определяется стоимость перевозок в каждый ПH B_j из всех ПО, и для ячейки B15 это записывается как (=СУММПРОИЗВ(B3:B6;B8:B11)), и для остальных аналогично.

Заметим, что сумма значений в ячейках B14:F14 равна сумме значений в ячейках J8:J11, что является необходимым и достаточным условием разрешимости транспорт ной задачи

Для решения поставленной задачи выбираем в меню Сервис опцию Поиск решения и заполняем открывшееся диалоговое окно (рис. 2).

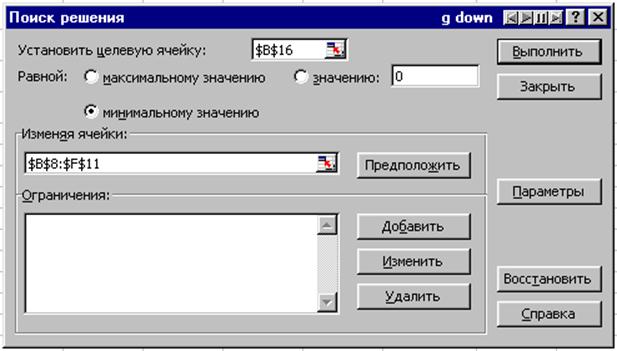
Рис. 2

Устанавливаем переключатель в положение «минимальному значению», так как будем исследовать целевую функцию на минимум. В качестве изменяемых значений ячеек выбираем матрицу перевозок (B8:F11).

Для ввода ограничений необходимо нажать кнопку Добавить. Сначала запишем условие неотрицательности перевозок , как показано на рис. 3.

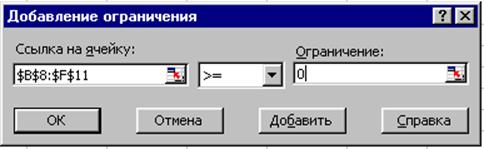
Рис. 3

Затем запишем m-условие (рис. 4).

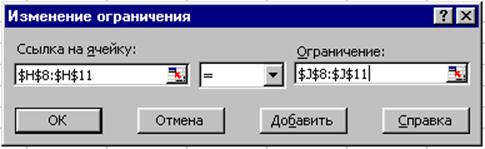
Рис. 4

Далее - n-условие (рис. 5).

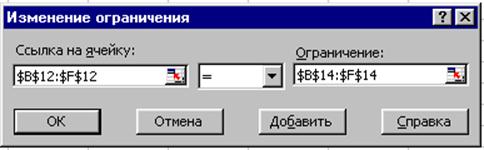
Рис. 5

Иногда исходя из смысла задачи необходимо еще накалывать условие целочисленности на переменные (рис. 6).

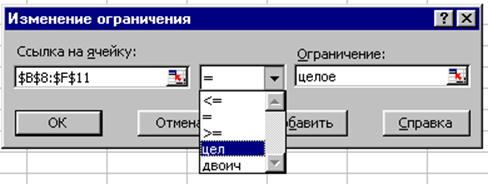
Рис. 6

В итоге получим следующее заполненное окно Поиска решения, которое показано на рис. 7.

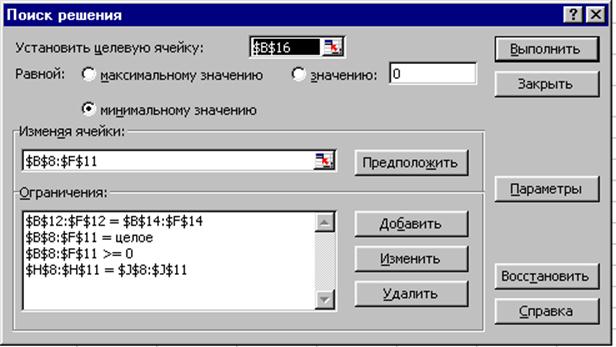
Рис. 7

После заполнения всех полей диалогового окна нажимаем кнопку Выполнить.

Когда решение найдено, в окне Excel (рис. 8) появляется соответствующее сообщение, а в ячейках B8:F11 устанавливаются значения, соответствующие оптимальному плану перевозок, и в ячейке B16 устанавливается минимальная общая стоимость всех перевозок. В данной задаче значение целевой функции равное 251.