Решение задач линейного программирования в соответствии с алгоритмом решения, так и с помощью пакета электронных таблиц Excel, страница 2

Пример: опорный план найдем методом северо-западного угла

ПН ПО	B1	B2	B3	B4	B5	Запасы  ai
A1	18	27	3			48
A2			30			30
A3			9	18		27
A4				4	16	20
A5					10	10
Заявки bj	18	27	42	22	26	135 135

r= m+n-1= 5+5-1=9;– расчетное количество базисных клеток;

= 9 – фактическое число базисных клеток;

Т.к. r= то найденный начальный план перевозок является опорным.

Метод потенциалов

Введением дополнительных переменных (потенциалов) упрощают процедуру связанную с вычислением в крайней точке вектора оценок , по которым можно судить об оптимальности в крайней точке или находить новый вектор базиса при решении ТЗ.

При решении ТЗ любую разность можно представить в виде:

                        (5)

где m+n-1 однозначно находят по индексу k l в каждой точке.

Представим каждое из чисел  через сумму переменных u_i  и v_j , которые назовем потенциалами и запишем в следующем виде:

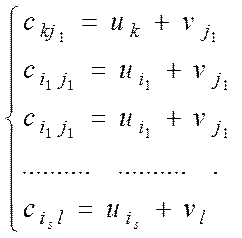                                                                    (6)

Представим систему m+n-1 уравнений относительно m+n неизвестных u_i , v_j. Придадим одному из потенциалов некоторое значение, например, u_k=0, тогда из уравнения (6) найдем однозначно:

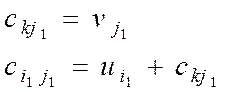
Таким образом, продолжаем до числа конца. Если в (5) подставим значения , выбранные в формуле (6), то получим следующую формулу являющуюся - основной формулой метода потенциалов:

.                                                                                  (7)

Алгоритм метода потенциалов.

Шаг1: проверка выполнения условия баланса;

Шаг2: определение начального плана ТЗ;

Шаг3: из уравнения (5) по известным c_st, стоящим в клетках, которые соответствуют базисным векторам, находят потенциалы u_i , v_j.

Шаг4: по формуле (6) вычисляем разности  для клетки с индексом k l;

Шаг5: определяем максимальную разность . Если она отрицательная, то рассматриваемая крайняя точка является оптимальной, в противном случае по правилу распределительного метода переходим к следующей крайней точке.

Через конечное число шагов получим решение, которое и будет являться оптимальным планом перевозок.

Пример:  решить ТЗ методом потенциалов:

ПН ПО	B1	B2	B3	B4	B5		запасы     ai	ui
A1	1  15	3  25	2  10	4	5		50	0
A2	3	1	5  26	3  10	2  4		40	3
A3	4	2	1	5	1  60		60	2
A4	2	3	1	2	4 21		21	5
заявки       bj	15	25	36	10	85		171
vj	1	3	2	0	-1

Применяя метод северо-западного угла найдем допустимый план перевозок. Проверим является найденный план опорным, для этого определим:

r=m+n-1= 4+5-1=8 – расчетное количество базисных клеток;

= 8 – фактическое число базисных клеток;

Т.к. r= то найденный начальный план перевозок является опорным.

Найдем значение целевой функции при данном плане:

L= 15+75+20+130+30+8+60+84=422;

Т.к. c_ij = u_i+v_j то следовательно можно записать, что u_i =c_ij-v_j, и v_j= c_ij-u_ij.

Принимаем в соответствии с алгоритмом u₁=0.

У нас клетка {1,1} является базисной и значение c₁₁=1, можем найти v₁, как v₁= c₁₁ - u₁=1-0=1;

И так далее v₂=3-0 =3; v₃= 2-0=2;  u₂=5-2=3;  v₄=3-3=0;  v₅=2-3= -1;  u₃=1-(-1)=2;  u₅=4-(-1)=5;

Применяя формулу (7) для пустых клеток, получаем:

=0+0-4= -4; =-1+0-5=-6; =1+3-3= 1; =3+3-1=5;   =1+2-4= -1;

=3+2-2=3; =2+2-1= 3; =0+2-5= -3; =1+5-2= 4; =3+5-3= 5;

=2+5-1=6; =0+5-2=3;

Находим максимальную разность , которая соответствует  - следовательно данная ячейка будет выводится из базиса. Для базисной ячейки составим цепочку a^st = a⁴³= {4,3},{4,5},{2,5},{2,3}. Найдя минимальное значение перевозки х_ij стоящее на концах горизонтальных звеньев (x_pq= x ₄₅=21) найдем ячейку, которую будем выводить из базиса (a ^pq = a⁴⁵).

Затем применим правила пересчета транспортной таблицы:

1. (x_st)_нов.=(x_pq)_стар

2. (x_ij)_нов.=(x _ij)_стар.-x_pq

Если клетка X _ij лежит на конце горизонтального звена цепочки, построенной для клетки  st , то выполняется это условие;  

3. (x_ij)_нов.=(x _ij)_стар.+x_pq

Есликлетка X _ij лежит на конце вертикального звена цепочки, построенной для клетки  st , то выполняется это условие;

4. (x_ij)_нов.=(x _ij)_стар                                                

Выполняется это условие, если в непустой клетке x _ij в предыдущей транспортной таблицы цепочка не терпит разрыва (или изгиба).

В итоге получим следующую транспортную таблицу

ПН ПО	B1	B2	B3	B4	B5		запасы     ai	ui
A1	1  15	3  25	2  10	4	5		50	0
A2	3	1	5  5	3  10	2  25		40	3
A3	4	2	1	5	1  60		60	2
A4	2	3	1  21	2	4		21	-1
заявки       bj	15	25	36	10	85		171
vj	1	3	2	0	-1