Нахождение отличные от тождественного нуля решения дифференциального уравнения, страница 8

uu2=simplify(subs(u, r, R2))  

uu2 =

40139127974558613/18014398509481984*pi-5685155742487199/562949953421312*log(2)-5734161139222659/220676381741154304*pi*cos(7*x)+1911387046407553/54043195528445952*pi*cos(6*x)-1911387046407553/13510798882111488*pi*cos(3*x)-5734161139222659/112589990684262400*pi*cos(5*x)+5734161139222659/72057594037927936*pi*cos(4*x)+1911387046407553/216172782113783808*pi*cos(12*x)+5734161139222659/18014398509481984*pi*cos(2*x)+5734161139222659/288230376151711744*pi*cos(8*x)-47389761481179/4503599627370496*pi*cos(11*x)+5734161139222659/450359962737049600*pi*cos(10*x)-1911387046407553/121597189939003392*pi*cos(9*x)-5734161139222659/4503599627370496*pi*cos(x)+1911387046407553/18014398509481984*pi^3  

График функции f1:

ezplot(f1,-3,3)

  

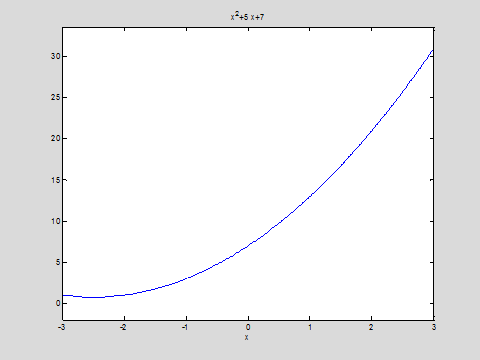
График решения:

ezplot(uu1,-3,3)  

  

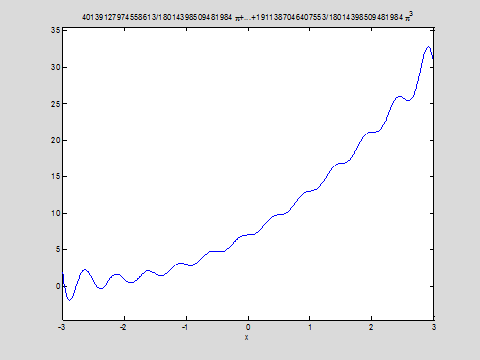
График общего решения:

ezsurf(u)  

  

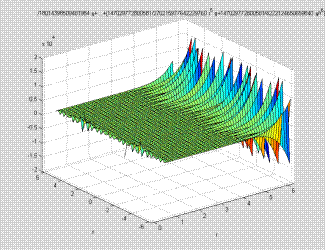
График функции f2:

ezplot(f2,-3,3)  

  

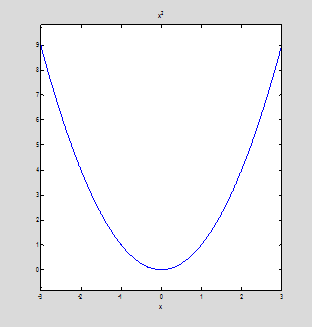
График решения:

ezplot(uu2,-3,3) 

  

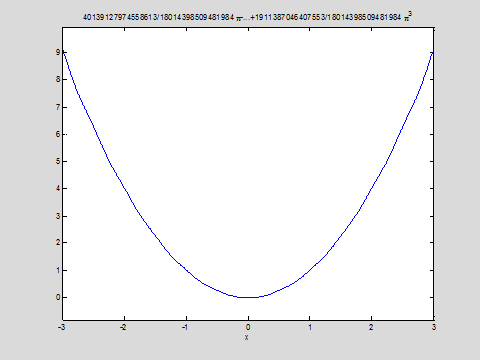
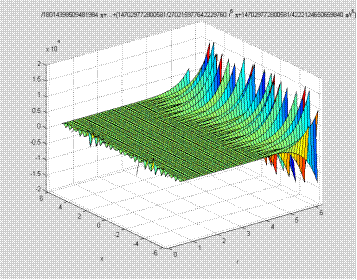
График общего решения:

ezsurf(u)  

Найти функцию, удовлетворяющую внутри круга уравнению Гельмгольца и принимающую на границе круга заданное значение.

,  ,   .

Введем полярную систему координат  с началом в центре круга. Тогда исходное уравнение примет вид

.

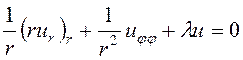Применим метод разделения переменных для отыскания частного решения этого уравнения:

.

Подставим и получим

.

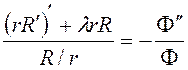Аналогично задаче Дирихле для уравнения Лапласа в круге, обозначим постоянную отношения через  и получим два обыкновенных дифференциальных уравнения:

,    ,

,    .

Первое уравнение имеет частное решение , где , . Положим . Преобразуем второе уравнение, подставив . Получим

уравнение Бесселя. Его решением, конечным во всем круге, включая начало координат, будет , где  – функция Бесселя 1-го рода n-го порядка.

Введем обозначения для коэффициентов и искомых функций:

syms f r x r0 Fn n u0 u1 u2 u  

Определяем граничное условие:

f=0  

f =

0  

r0=2  

r0 =

2  

Определяем часть решения:

Fn=cos(n*x)+sin(n*x)  

Fn =

cos(n*x)+sin(n*x)  

Для отыскания нескольких положительных корней построим графики функций Бесселя и определим корни:

ezplot(besselj(0,x),0,20)  

  

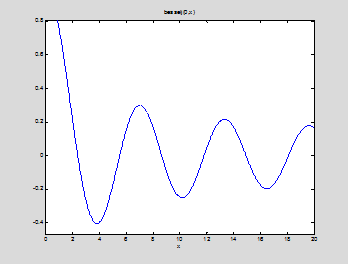
fzero('besselj(0,x)',[1,4])  

ans =

2.4048  

ezplot(besselj(1,x),0,20)  

  

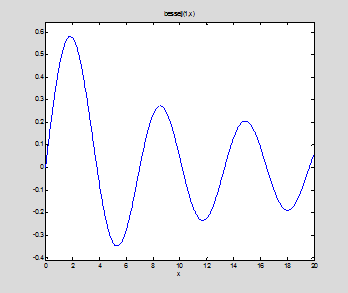
fzero('besselj(1,x)',[1,4])  

ans =

3.8317  

ezplot(besselj(2,x),0,20)  

  

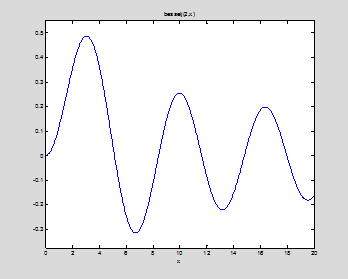
fzero('besselj(2,x)',[3,6])  

ans =

5.1356  

ezplot(besselj(3,x),0,20)  

  

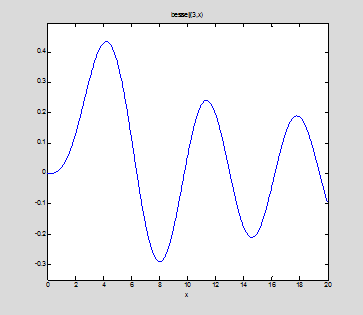
fzero('besselj(3,x)',[4,8])  

ans =

6.3802  

lam(1)=fzero('besselj(0,x)',[1,4])/r0;  

lam(2)=fzero('besselj(1,x)',[1,4])/r0;  

lam(3)=fzero('besselj(2,x)',[3,6])/r0;  

lam(4)=fzero('besselj(3,x)',[4,8])/r0;  

vpa(lam,10)  

ans =

[ 1.202412779, 1.915852985, 2.567811151, 3.190080948]  

u0=besselj(0,lam(1)*r)*subs(Fn,'n',0)  

u0 =

besselj(0,84612277230701/70368744177664*r)  

u1=besselj(1,lam(2)*r)*subs(Fn,'n',1)  

u1 =

besselj(1,8628234789809931/4503599627370496*r)*(cos(x)+sin(x))  

u2=besselj(2,lam(3)*r)*subs(Fn,'n',2)  

u2 =

besselj(2,2891098335610663/1125899906842624*r)*(cos(2*x)+sin(2*x))  

u3=besselj(3,lam(4)*r)*subs(Fn,'n',3)  

u3 =

besselj(3,897927960532709/281474976710656*r)*(cos(3*x)+sin(3*x))  

Решение уравнения:

u=u0+u1+u2+u3  

u =

besselj(0,84612277230701/70368744177664*r)+besselj(1,8628234789809931/4503599627370496*r)*(cos(x)+sin(x))+besselj(2,2891098335610663/1125899906842624*r)*(cos(2*x)+sin(2*x))+besselj(3,897927960532709/281474976710656*r)*(cos(3*x)+sin(3*x))