28670805696113295/18014398509481984*pi+2*cos(2*x)-8*sin(x)*pi-3*sin(2*x)+17202483417667977/18014398509481984*pi^2+8/49*cos(7*x)-6/7*sin(7*x)+1911387046407553/2251799813685248*pi^3-2*sin(3*x)+8/9*cos(3*x)+1/8*cos(8*x)-3/4*sin(8*x)-6*sin(x)+1/2*cos(4*x)+8*cos(x)-3/2*sin(4*x)+8/81*cos(9*x)+8/25*cos(5*x)-6/5*sin(5*x)-2/3*sin(9*x)+2/25*cos(10*x)-3/5*sin(10*x)+2/9*cos(6*x)-sin(6*x)-4*sin(2*x)*pi-8/3*sin(3*x)*pi-2*sin(4*x)*pi-8/5*sin(5*x)*pi-4/3*sin(6*x)*pi-8/7*sin(7*x)*pi-sin(8*x)*pi-8/9*sin(9*x)*pi-4/5*sin(10*x)*pi
График функции:
ezplot(f,0,7)
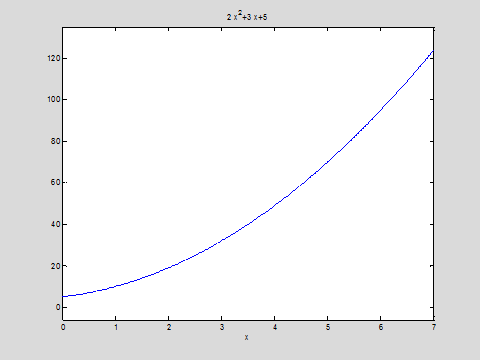
График решения:
ezplot (uu,0,6)
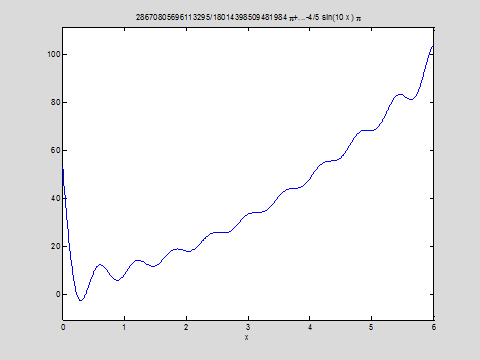
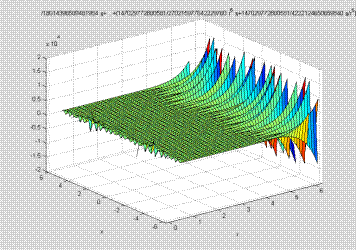
График общего решения:
ezsurf(u)
Решить задачу Дирихле для уравнения Лапласа в кольце.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Общее решение поставленной задачи будем искать в виде суперпозиции гармонических функций (функций, удовлетворяющих уравнению Лапласа). В качестве таких функций выберем следующие (см. решение задачи Дирихле для уравнения Лапласа в круге):
1) 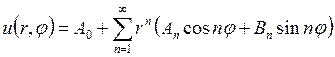 –
общее решение внутренней задачи Дирихле для уравнения Лапласа в круге. Эта
функция по отношению к внешнему радиусу кольца является решением внутренней
задачи.
–
общее решение внутренней задачи Дирихле для уравнения Лапласа в круге. Эта
функция по отношению к внешнему радиусу кольца является решением внутренней
задачи.
2) 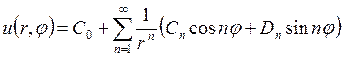 –
общее решение внешней задачи Дирихле для уравнения Лапласа в круге. Эта функция
по отношению к внутреннему радиусу кольца является решением внешней задачи.
–
общее решение внешней задачи Дирихле для уравнения Лапласа в круге. Эта функция
по отношению к внутреннему радиусу кольца является решением внешней задачи.
3) ![]() –
фундаментальное решение уравнения Лапласа на плоскости, является всюду
гармонической, кроме
–
фундаментальное решение уравнения Лапласа на плоскости, является всюду
гармонической, кроме ![]() .
.
Таким образом, общее решение поставленной задачи будем искать в виде:
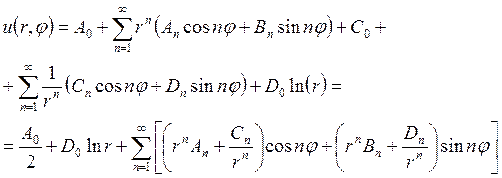
где в последнем равенстве переобозначили 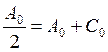 .
.
Для отыскания неизвестных коэффициентов применим граничные условия:
1) ![]() ,
где
,
где ![]() – внутренний радиус
кольца. Разложим
– внутренний радиус
кольца. Разложим ![]() в ряд Фурье:
в ряд Фурье:
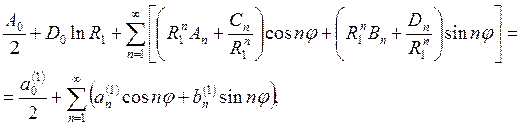
откуда, приравняв коэффициенты, получим
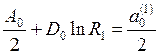 ,
,
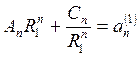 , (1)
, (1)
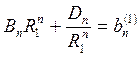 .
.
2) ![]() ,
где
,
где ![]() – внешний радиус кольца.
Аналогично, получим
– внешний радиус кольца.
Аналогично, получим
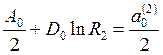 ,
,
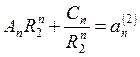 , (2)
, (2)
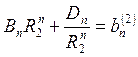 .
.
Решая полученную систему из уравнений (1) и (2), получаем:
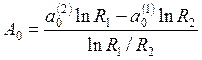 ,
,
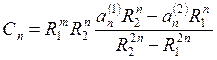 ,
,
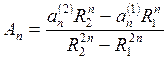 , (3)
, (3)
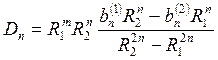 ,
,
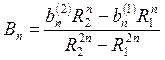 ,
,
Коэффициенты ![]() ,
,
![]() ,
, ![]() ,
, ![]() определяются следующим образом:
определяются следующим образом:
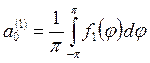 ,
,
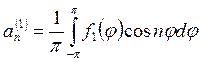 ,
,
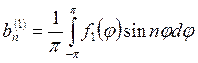 ,
,
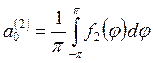 ,
,
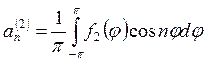 ,
,
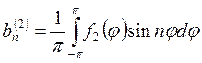
Введем обозначения для коэффициентов и искомых функций:
syms R1 R2 an1 an2 A0 Cn An Dn D0 Bn bn1 bn2 uu1 uu2 f1 f2
Определяем граничное условие:
f1=x^2+5*x+7
f1 =
x^2+5*x+7
f2=x^2
f2 =
x^2
R1=1
R2=2
R1 =
1
R2 =
2
Вычисляем коэффициенты:
a01=1/pi*int(f1,x,-pi,pi)
a01 =
1911387046407553/9007199254740992*pi^3+40139127974558613/9007199254740992*pi
an1=1/pi*int(f1*cos(n*x),x,-pi,pi)
an1 =
5734161139222659/9007199254740992*(n^2*pi^2*sin(pi*n)-2*sin(pi*n)+2*pi*n*cos(pi*n)+7*sin(pi*n)*n^2)/n^3
bn1=1/pi*int(f1*sin(n*x),x,-pi,pi)
bn1 =
-28670805696113295/9007199254740992*(-sin(pi*n)+pi*n*cos(pi*n))/n^2
a02=1/pi*int(f2,x,-pi,pi)
a02 =
1911387046407553/9007199254740992*pi^3
an2=1/pi*int(f2*cos(n*x),x,-pi,pi)
an2 =
5734161139222659/9007199254740992*(n^2*pi^2*sin(pi*n)-2*sin(pi*n)+2*pi*n*cos(pi*n))/n^3
bn2=1/pi*int(f2*sin(n*x),x,-pi,pi)
bn2 =
0
A0=(a02*log(R1)-a01*log(R2))/log(R1/R2)
A0 =
1911387046407553/9007199254740992*pi^3+40139127974558613/9007199254740992*pi
Cn=subs(R1^n*R2^n*(an1*R2^n-an2*R1^n)/(R2^(2*n)-R1^(2*n)),[R1,R2],[1,2])
Cn =
2^n*((27227927363807715762992813480013/2535301200456458802993406410752*sin(pi*n)*n^2-5734161139222659/4503599627370496*sin(pi*n)+5734161139222659/4503599627370496*pi*n*cos(pi*n))/n^3*2^n-(15929767251982789428336599799885/2535301200456458802993406410752*sin(pi*n)*n^2-5734161139222659/4503599627370496*sin(pi*n)+5734161139222659/4503599627370496*pi*n*cos(pi*n))/n^3)/(2^(2*n)-1)
An=subs((an2*R2^n-an1*R1^n)/(R2^(2*n)-R1^(2*n)),[R1,R2],[1,2])
An =
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.