Нахождение отличные от тождественного нуля решения дифференциального уравнения, страница 2

B  (8)

z2_diff=simple(subs(ny_diff_if,lyambda2,1))  

z2_diff =

-B  

(9)

Решаем уравнения (8), (9) относительно A и B:

s2=solve(z2,z2_diff,B,A)  

Warning: 1 equations in 3 variables.

> In C:\PROGRAMM\MATLAB6p1\toolbox\symbolic\solve.m at line 110

In C:\PROGRAMM\MATLAB6p1\toolbox\symbolic\@sym\solve.m at line 49

s2 =

A: [1x1 sym]

B: [1x1 sym]  

s2.A  

ans =

A  

s2.B  

ans =

0  

Решить задачу Дирихле для уравнения Лапласа в круге.

,    ,   .

- оператор Лапласа. Уравнение  принадлежит к эллиптическому типу. Задача Дирихле для уравнения Лапласа заключается в нахождении функции , гармонической в области T и принимающей на границе этой области заданные значения. Существуют внутренняя и внешняя задачи Дирихле для уравнения Лапласа в круге. В данной работе решается внутренняя задача – отыскание неизвестной функции в круге. 

Введем в рассмотрение полярную систему координат  с началом в центре круга. Исходное уравнение, в полярных координатах, примет вид:

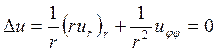.    (1)

Применим метод разделения переменных, т.е. будем искать решение этого уравнения в виде следующей функции:

. (2)

Подставим (2) в (1) и получим

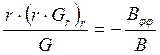  (3)

Левая часть (3) зависит от r, а правая – от . Такое равенство возможно только тогда, когда обе части есть постоянные величины, равные какому-то числу  (постоянной разделения). Приравняв части этой постоянной, получаем два уравнения:

             (4)

         (5)

Общее решение уравнения (4) имеет вид (см. задачу Штурма-Лиувилля):

, причем, поскольку при изменении угла  на величину, равную , функция  не должна измениться (т.е. ), то  – периодическая функция с тем же периодом. Но это возможно только при , , т.е.

(6)

Функцию  будем искать в виде

.           (7)

После подстановки (7) в (5) получим

, откуда следует (с учетом, что ), что . Поэтому

,   ,    .

Для решения внутренней задачи необходимо принять , поскольку при  и  функция  обращается в бесконечность, что является невозможным. Без ограничения общности положим , тогда . Подставим полученный результат и (6) в (2). Получим

(8)

Поскольку для всех n функции (8) представляют собой частные решения однородного уравнения (1), то сумма этих частных решения является общим решением

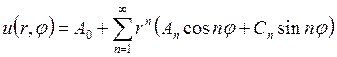     (9)

Для отыскания коэффициентов , ,  необходимо использовать граничное условие

.                   (10)

Для этого разложим функцию  в ряд Фурье

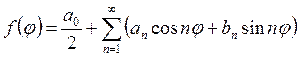  (11)

После подстановки (9) и (11) в (10), приравнивания коэффициентов при соответствующих слагаемых получаем следующие формулы:

,

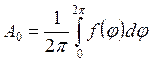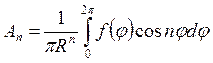,              (12)

.

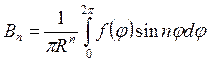Таким образом, решение задачи сводится к отысканию неизвестных коэффициентов  , , .

Введем обозначения для коэффициентов и искомых функций:

syms x A0 An Cn R n u1 u2 un u uu r

Определяем граничное условие:

f=2*x^2+3*x+5 

f =

2*x^2+3*x+5  

R=1 

R =

1  

Вычисляем коэффициенты:

A0=1/(2*pi)*int(f, 'x', 0, 2*pi)  

A0 =

1911387046407553/2251799813685248*pi^3+17202483417667977/18014398509481984*pi^2+28670805696113295/18014398509481984*pi  

An=subs(1/(R^n*pi)*int(f*cos(n*x), 'x', 0, 2*pi), 'R', 1)  

An =

2/pi*(8*n^2*pi^2*sin(pi*n)*cos(pi*n)-4*sin(pi*n)*cos(pi*n)+8*pi*n*cos(pi*n)^2-4*pi*n+3*n*cos(pi*n)^2-3*n+6*pi*n^2*sin(pi*n)*cos(pi*n)+5*n^2*sin(pi*n)*cos(pi*n))/n^3  

Cn=subs(1/(R^n*pi)*int(f*sin(n*x), 'x', 0, 2*pi), 'R', 1)  

Cn =

2/pi*(-8*n^2*pi^2*cos(pi*n)^2+4*n^2*pi^2+4*cos(pi*n)^2-4+8*pi*n*sin(pi*n)*cos(pi*n)+3*n*sin(pi*n)*cos(pi*n)-6*pi*n^2*cos(pi*n)^2+3*pi*n^2-5*n^2*cos(pi*n)^2+5*n^2)/n^3  

Определим несколько первых слагаемых:

un=r^n*(An*cos(n*x)+Cn*sin(n*x))  

un =