Нахождение отличные от тождественного нуля решения дифференциального уравнения

Министерство образования  и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Факультет Компьютерных технологий

Кафедра математического обеспечения и применения ЭВМ

РГЗ №2

По курсу «УМФ»

Выполнил студент группы 4ВС-1                                                                                                                                                 Кормин И.А.

Преподаватель                                                                                                                                                                                        Могильников Е.В.

Вариант:                                                                                                                                                                                                     3

Комсомольск-на-Амуре

2007

Задание:  I. Найти в указанной области отличные от тождественного нуля решения  дифференциального уравнения, удовлетворяющее заданным граничным условиям (задача Штурма-Лиувилля):

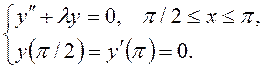
II. Решить задачу Дирихле для уравнения Лапласа в круге.

,    ,   .

III. Решить задачу Дирихле для уравнения Лапласа в кольце.

,   ,    ,   .

IV. Найти функцию, удовлетворяющую внутри круга уравнению Гельмгольца и принимающую на границе круга заданное значение.

,  ,   .

Задачи должны быть решены в системе Matlab.

Найти в указанной области отличные от тождественного нуля решения  дифференциального уравнения, удовлетворяющее заданным граничным условиям (задача Штурма-Лиувилля):

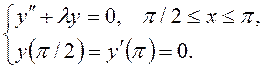
Данное уравнение при любом  имеет тривиальное решение , удовлетворяющее граничным условиям. Нетривиальные решения существуют не при всяких . Задача Штурма-Лиувилля заключается в определении значений этого параметра, при которых существуют нетривиальные решения данного уравнения. Значение , при котором уравнение имеет нетривиальное решение, называется собственным значением, а само решение  – соответствующей  собственной функцией.

Из курса ОДУ известно, что вид общего решения исходного уравнения зависит от знака . Рассмотрим несколько случаев.

1) , тогда общее решение имеет вид

           

Определим необходимые переменные:

syms A B lyambda lyambda2 det1 det2 

Запишем общее решение:

y=A*exp((-sqrt(-lyambda))*x)+B*exp(sqrt(-lyambda)*x) 

y =

A*exp(-(-lyambda)^(1/2)*x)+B*exp((-lyambda)^(1/2)*x)  

Продиффиринцируем его:

y_diff_x=diff(y,x)  

y_diff_x =

-A*(-lyambda)^(1/2)*exp(-(-lyambda)^(1/2)*x)+B*(-lyambda)^(1/2)*exp((-lyambda)^(1/2)*x)  

Из начальных условий получим:

при x=:

y_if=subs(y,x,pi/2)  

y_if =

A*exp(-1/2*(-lyambda)^(1/2)*pi)+B*exp(1/2*(-lyambda)^(1/2)*pi)  (1)

при x=:

y_diff_if=subs(y_diff_x,x,pi) 

y_diff_if =

-A*(-lyambda)^(1/2)*exp(-(-lyambda)^(1/2)*pi)+B*(-lyambda)^(1/2)*exp((-lyambda)^(1/2)*pi)  (2)

Рассмотрим совместно уравнения (1) и (2) как систему уравнений относительно перменных А и В.

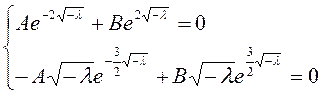
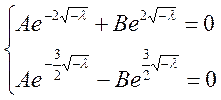                  (3)

Найдем определитель системы (3):

det1=det([exp(-2*(-lyambda)^(1/2)),exp(2*(-lyambda)^(1/2)); exp(-3/2*(-lyambda)^(1/2)),exp(3/2*(-lyambda)^(1/2))]) 

det1 =

exp(-2*(-lyambda)^(1/2))*exp(3/2*(-lyambda)^(1/2))-exp(2*(-lyambda)^(1/2))*exp(-3/2*(-lyambda)^(1/2))  

Упрощаем:

[R,H]=simple(det1) 

R =

exp(-1/2*(-lyambda)^(1/2))-exp(1/2*(-lyambda)^(1/2))

H =

combine  

Получаем определитель равен: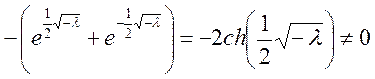

т.к. функция ch(x) не имеет нулей.

Система (3) – система однородных линейных уравнений. Поскольку определитель отличен от нуля, то она имеет только тривиальное решение А=В=0. Подставив константы в общее решение, получим . Это решение не представляет интереса.

2)  , тогда общее решение имеет вид

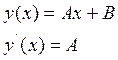
Подставляя в полученные уравнения начальные условия получим:

при x=:

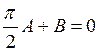         (4)

при x=:

Подставляя А=0 в уравнение (4) получаем В=0. Получаем тривиальное решение .

3) , тогда общее решение имеет вид

ny=A*cos(sqrt(lyambda2)*x)+B*sin(sqrt(lyambda2)*x) 

ny =

A*cos(lyambda2^(1/2)*x)+B*sin(lyambda2^(1/2)*x)  

Продиффиринцируем его:

ny_diff_x=diff(ny) 

ny_diff_x =

-A*sin(lyambda2^(1/2)*x)*lyambda2^(1/2)+B*cos(lyambda2^(1/2)*x)*lyambda2^(1/2)  

Из начальных условий получим:

при x=:

ny_if=subs(ny,x,pi/2)  

ny_if =

A*cos(1/2*lyambda2^(1/2)*pi)+B*sin(1/2*lyambda2^(1/2)*pi)  (5)

при x=:

ny_diff_if=subs(ny_diff_x,x,pi)  

ny_diff_if =

-A*sin(lyambda2^(1/2)*pi)*lyambda2^(1/2)+B*cos(lyambda2^(1/2)*pi)*lyambda2^(1/2)  

(6)

Рассмотрим совместно уравнения (5) и (6) как систему однородных линейных уравнений относительно А и В.

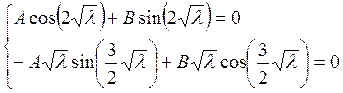
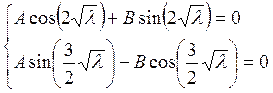        (7)

Найдем определитель системы (7)

det2=det([cos(1/2*lyambda2^(1/2)*pi),sin(1/2*lyambda2^(1/2)*pi);-sin(lyambda2^(1/2)*pi)*lyambda2^(1/2),cos(lyambda2^(1/2)*pi)*lyambda2^(1/2)])

det2 =

cos(1/2*lyambda2^(1/2)*pi)*cos(lyambda2^(1/2)*pi)*lyambda2^(1/2)+sin(1/2*lyambda2^(1/2)*pi)*sin(lyambda2^(1/2)*pi)*lyambda2^(1/2)  

Упрощаем:

[R,H]=simple(det2)  

R =

lyambda2^(1/2)*cos(1/2*lyambda2^(1/2)*pi)

H =

combine  

Для существования не тривиальных решений, определитель должен быть равен нулю

solve(R, lyambda2)

ans =

[ 0]

[ 1]  

При

z2=simple(subs(ny_if,lyambda2,1))  

z2 =