МПС РФ
Петербургский Государственный Университет Путей Сообщения
Кафедра: «Высшая математика»
Курсовой проект
Вариант №9
Выполнил студент
Группы ЭТ-302
Екимов Д. А.
Санкт-Петербург
2004г
2. Задание к курсовой работе
1. Выразить событие А, состоящее в отказе схемы, через события Аi- отказ i- го элемента (i= 1,2,…,6). Составить формулу для определения вероятности отказов её элементов Qi.
2. Составить таблицы значений функций распределения вероятностей отказов системы Q(t) и функции распределения вероятности безотказной работы P(t) для tε[0,tг] с заданным шагом ∆t. Значение tг получено из условия:
Q(tг)>=0,997.
Составить таблицу значений плотности вероятности отказа системы
f(t)=dQ(t)/dt,
используя простейшую форму численного дифференцирования f(t)=∆Qк/∆t=(Q(tк+1)-
Q(tк)) /∆t, к=0,1,2,…,(n-1).
Построить графики функций Q(t),P(t),f(t). Графически найти моду Mo и медиану
Me случайной величины T.
3. Вычислить математическое ожидание MT, дисперсию DT и среднее квадратичное отклонение σ случайной величины наработки системы до отказа.
4. Определить вероятность безотказной работы системы в течение t1>=200ч, t2>=500ч, t3>=1000ч по графику функции Q(t) или P(t).
Определить γ – процентный ресурс системы для γ1=0,1; γ2=0,05; γ3=0,01.
γ– процентный ресурс t, определяется как графическое решение уравнения
Q(tг )= γ.
5. Записать формулу для вычисления наработки системы до отказа по заданным наработкам до отказа её элементов. Произвести упорядочение заданной выборки из генеральной совокупности –наработки системы до отказа, построить вариационный ряд. Записать распределение выборки и построить гистограмму относительных частот.
Найти оценки математического ожидания S случайной величины.
6. Найти доверительные интервалы для математического ожидания с доверительными вероятностями γ1=0,9; γ2=0,95; γ3=0,99; указать точность полученных оценок.
7. Проверить гипотезу Ho о виде распределения вероятности отказа системы с помощью критерия χ^2 (Пирсна). В качестве теоретического распределения принять распределение. Уровень значимости принять равным λ1=0,1; λ2=0,05; λ3=0,01.
Исходные данные:
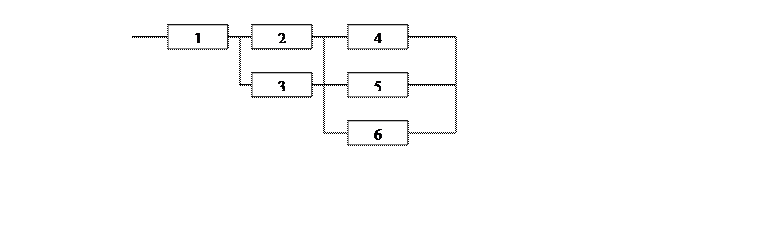
1) Отказ системы (Событие А)
A1,A2,…,A6- Выход из строя соответствующего элемента схемы
A- Выход из строя схемы
A=A1 ∩ (A2UA3) ∩ (A4UA5UA6)
Вероятность отказа системы
Q=1-Q1(1-(1-Q2)(1-Q3))(1-(1-Q4)(1-Q5)(1-Q6))
Qi- вероятность отказа i-го элемента системы.
2) Таблица значений функций Q(t),P(t),f(t).
|
функция распределения вероятности отказов схемы |
||||
|
T |
Q |
f(t) |
P |
|
|
50 |
0,001068105 |
6,04997E-05 |
0,998931895 |
|
|
100 |
0,004093089 |
9,46747E-05 |
0,995906911 |
|
|
150 |
0,008826824 |
0,000124401 |
0,991173176 |
|
|
200 |
0,01504687 |
0,000150144 |
0,98495313 |
|
|
250 |
0,02255409 |
0,000172362 |
0,97744591 |
|
|
300 |
0,0311722 |
0,000191745 |
0,9688278 |
|
|
350 |
0,04075947 |
0,000209987 |
0,95924053 |
|
|
400 |
0,0512588 |
0,000230945 |
0,9487412 |
|
|
450 |
0,06280603 |
0,00026111 |
0,93719397 |
|
|
500 |
0,07586154 |
0,00030827 |
0,92413846 |
|
|
550 |
0,09127506 |
0,000378607 |
0,90872494 |
|
|
600 |
0,1102054 |
0,000473792 |
0,8897946 |
|
|
650 |
0,133895 |
0,000589658 |
0,866105 |
|
|
700 |
0,1633779 |
0,000716938 |
0,8366221 |
|
|
750 |
0,1992248 |
0,00084354 |
0,8007752 |
|
|
800 |
0,2414018 |
0,000957274 |
0,7585982 |
|
|
850 |
0,2892655 |
0,00104814 |
0,7107345 |
|
|
900 |
0,3416725 |
0,00110965 |
0,6583275 |
|
|
950 |
0,397155 |
0,00113918 |
0,602845 |
|
|
1000 |
0,454114 |
0,001137556 |
0,545886 |
|
|
1050 |
0,5109918 |
0,001108198 |
0,4890082 |
|
|
1100 |
0,5664017 |
0,001056148 |
0,4335983 |
|
|
1150 |
0,6192091 |
0,000987124 |
0,3807909 |
|
|
1200 |
0,6685653 |
0,00090682 |
0,3314347 |
|
|
1250 |
0,7139063 |
0,000820406 |
0,2860937 |
|
|
1300 |
0,7549266 |
0,000732222 |
0,2450734 |
|
|
1350 |
0,7915377 |
0,000645698 |
0,2084623 |
|
|
1400 |
0,8238226 |
0,000561734 |
0,1761774 |
|
|
1450 |
0,8519093 |
0,000488424 |
0,1480907 |
|
|
1500 |
0,8763305 |
0,000417146 |
0,1236695 |
|
|
1550 |
0,8971878 |
0,000354744 |
0,1028122 |
|
|
1600 |
0,914925 |
0,00029963 |
0,085075 |
|
|
1650 |
0,9299065 |
0,000251542 |
0,0700935 |
|
|
1700 |
0,9424836 |
0,000210008 |
0,0575164 |
|
|
1750 |
0,952984 |
0,00017445 |
0,047016 |
|
|
1800 |
0,9617065 |
0,000144252 |
0,0382935 |
|
|
1850 |
0,9689191 |
0,000118772 |
0,0310809 |
|
|
1900 |
0,9748577 |
9,7408E-05 |
0,0251423 |
|
|
1950 |
0,9797281 |
8,1386E-05 |
0,0202719 |
|
|
2000 |
0,9837974 |
6,299E-05 |
0,0162026 |
|
|
2050 |
0,9869469 |
5,2564E-05 |
0,0130531 |
|
|
2100 |
0,9895751 |
4,25E-05 |
0,0104249 |
|
|
2150 |
0,9917001 |
0,000034246 |
0,0082999 |
|
|
2200 |
0,9934124 |
2,7504E-05 |
0,0065876 |
|
|
2250 |
0,9947876 |
2,2016E-05 |
0,0052124 |
|
|
2300 |
0,9958884 |
1,7564E-05 |
0,0041116 |
|
|
2350 |
0,9967666 |
1,3964E-05 |
0,0032334 |
|
|
2400 |
0,9974648 |
1,1064E-05 |
0,0025352 |
|
|
2450 |
0,998018 |
0,001982 |
||
3) Математическое ожидание и дисперсия:
МТ=∫Р(t) dt= 1006,792629
MT^2= 1269540,022
DT=MT^2-(MT)^2= 255908,6242
δ= DT^(1/2)= 505,874
4) Вероятность безотказной работы и γ-ресурс
P(t≥200)= 0,98495313 t0,1=550
P(t≥500)= 0,92413846 t0,05=400
P(t≥1000)= 0,545886 t0,01=175
5) Наработка системы до отказа
Выборка (n=50):1299 1168 1862 1326 544 1224 1023 694 272 1309 679 482 896 1269 1539 1306 1975 1124 1606 953 736 830 910 811 861 1332 1620 894 1471 1001 1227 563 1151 1079 1420 1331 863 983 900 871 1116 646 773 1153 812 763 1098 561 622 954
Вариационный ряд: 272 482 544 561 563 622 646 679 694 736 763 773 811 812 830 861 863 871 894 896 900 910 953 954 983 1001 1023 1075 1079 1098 1116 1124 1151 1153 1168 1224 1227 1269 1299 1306 1309 1326 1331 1332 1420 1471 1539 1606 1620 1862
Интервал: tε[272;1862].
Число частичных интервалов:K=6
Величина частичного интервала
h= (1862-272)/6=265
Распределение выборки:
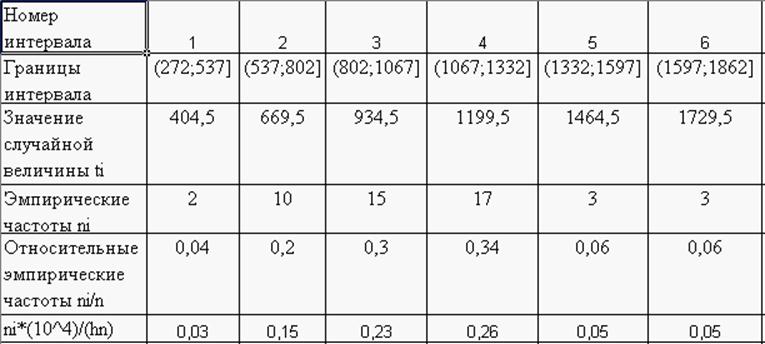
∑ni=30 ∑ni/n=1
Выборочное среднее: t=0,03*404,5+0,15*669,5+0,23*934,5+0,26*1199,5+0,05*1464,5+0,05*1729,5=799,065
Выборочная дисперсия: S^2=t^2-(t)^2
t^2=0,03*(404,5)^2+0,15*(669,5)^2+0,23*(934,5)^2+0,26*(1199,5)^2+0,05*(1464,5)^2+0,05*(1729,5)^2=903884,5
S^2=903884,5-(799,065)^2=265379,6
Выборочное среднее квадратичное отклонение: S=515,15
6) Доверительные для математического ожидания: (a1;a2)
|
γ |
t |
δ =t*s/(n^0,5) |
a1 |
a2 |
|
0,9 |
||||
|
0,95 |
||||
|
0,99 |
7) Проверка гипотезы Ho по критерию χ^2
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
|
Границы интервала |
(272;537] |
(537;802] |
(802;1067] |
(1067;1332] |
(1332;1597] |
(1597;1862] |
|
Эмпирические частоты ni |
2 |
10 |
15 |
17 |
3 |
3 |
|
Теоретические частоты n*Pi |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.