Алгоритм с программой расчета мощностей и возможности обработки на фрезерных станках, страница 4

Кодировочная таблица типа станка (ТС):

ТС=0   - станок с прямолинейной подачей;

TС=1   - ставок с круговой подачей.

Кодировочная таблица типа фрезы и материала ее режущей части (ТФМ):

ТФМ=0  - торцевая твердосплавная;

ТФМ=1  - дисковая для обработки плоскостей твердосплавная;

ТФМ=2  - дисковая для обработки пазов твердое плавная (в т.ч. с составными ножами);

ТФМ=3   - торцевая быстрорежущая;

ТФМ=4  - дисковая для обработки плоскостей быстрорежущая (в т.ч.

цельная);

ТФМ=5  - дисковая для обработки пазов быстрорежущая;

ТФМ=6   - прорезная быстрорежущая;

ТФМ=7  - концевая для обработки пазов быстрорежущая;

ТФМ=8  - цилиндрическая и концевая быстрорежущая;

ТФМ=9    -радиусная выпуклая быстрорежущая;

TФM=10 - радиусная вогнутая быстрорежущая;

TФM=11 - двухугловая быстрорежущая;

ТФМ=12 - для пазов сегментных шпонок быстрорежущая.

Кодировочная таблица обрабатываемого материала (КОМ):

КОМ=0 - сталь;

KOM=1 - алюминиевые сплавы;

КОМ=2 - серый чугун;

КОМ=3 - ковкий чугун.

При этих условиях реализация блока 5 рисунок 3.1 с учетом некоторых вариантов решения поставленных вопросов может быть фрагментально представлена в виде рисунка 3.5. При этом принято, что значения переменным D, t, Sz и z присвоены ранее.

Математическая модель для блока 6 и 7 рисунок 3.1 может   бить представлена следующими зависимостями:

- основное машинное время обработки tм в мин

,

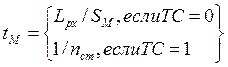- фактическая величина подачи на зуб фрезы Sz мм/зуб (по принятым режимам резания)   

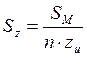, если ТС=0

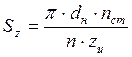, если TC=1

где - наибольший диаметр расположения деталей на столе станка.

Данный фрагмент математической модели может быть представлен схемой алгоритма, изображенной на рисунке. 3.6.

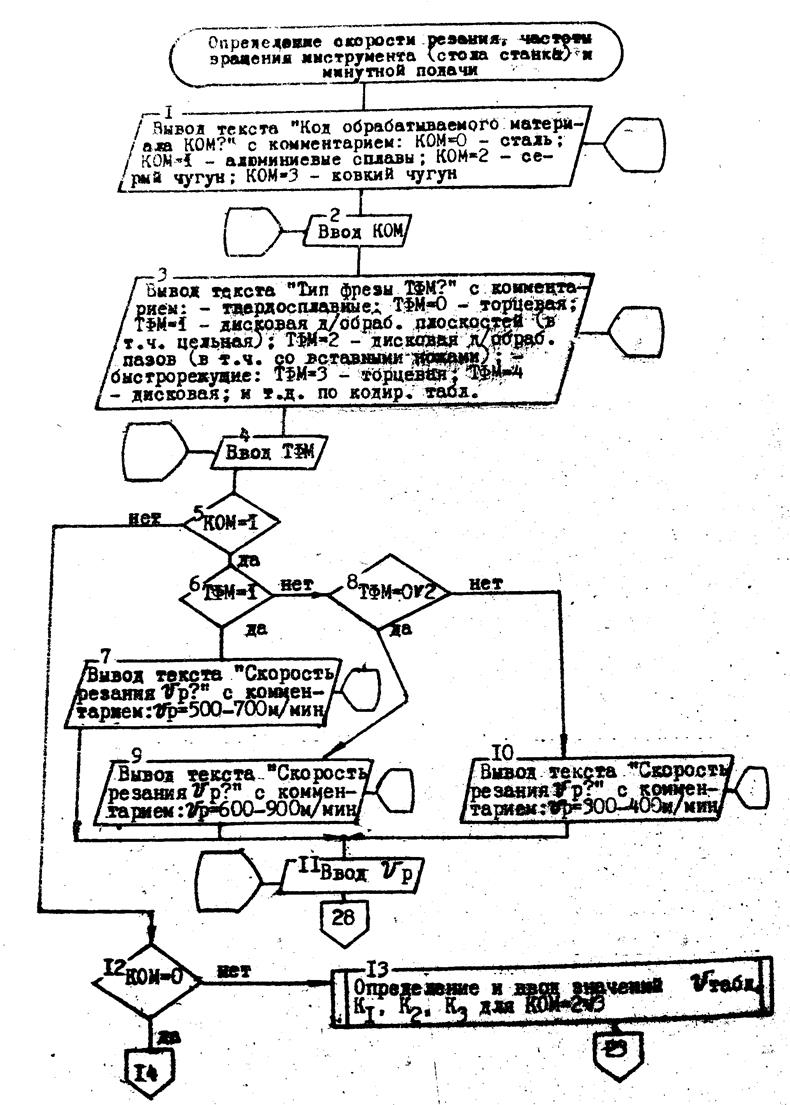
Рисунок 3.5 Схема алгоритма, реализующая блок 5 (Рисунок 3.1)

        

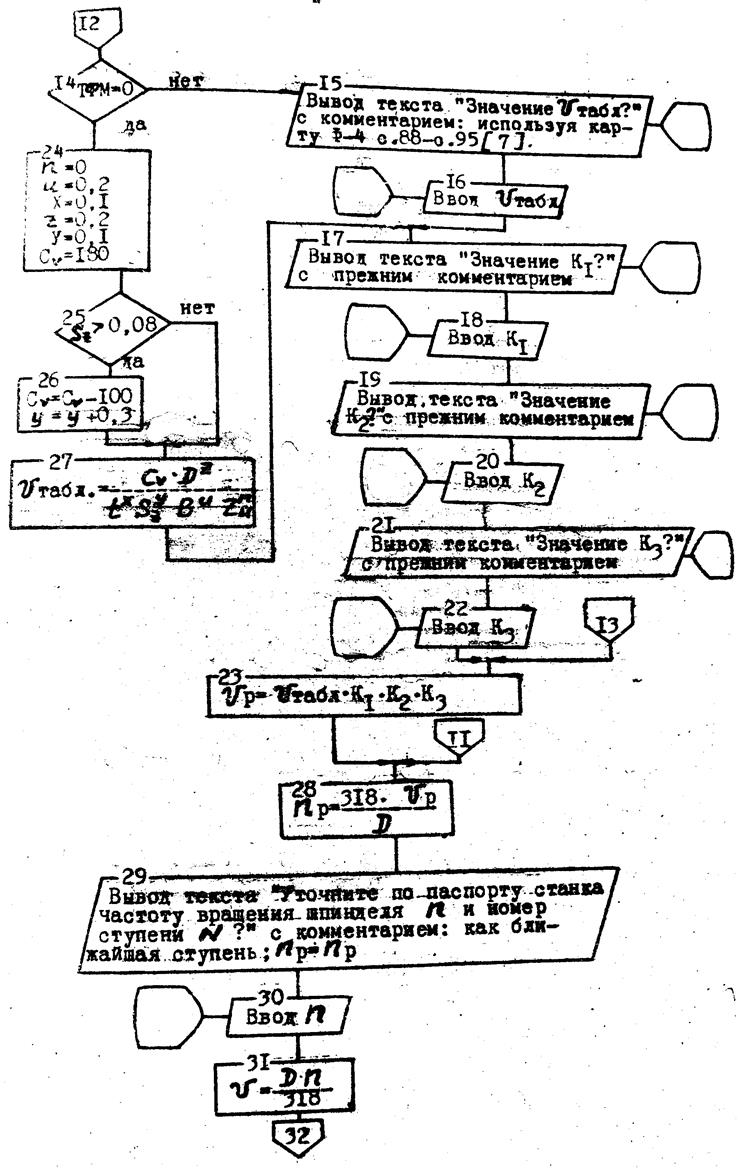
Рисунок 3.5 Схема алгоритма, реализующая блок 5 (Рисунок 3.1)

продолжение

         

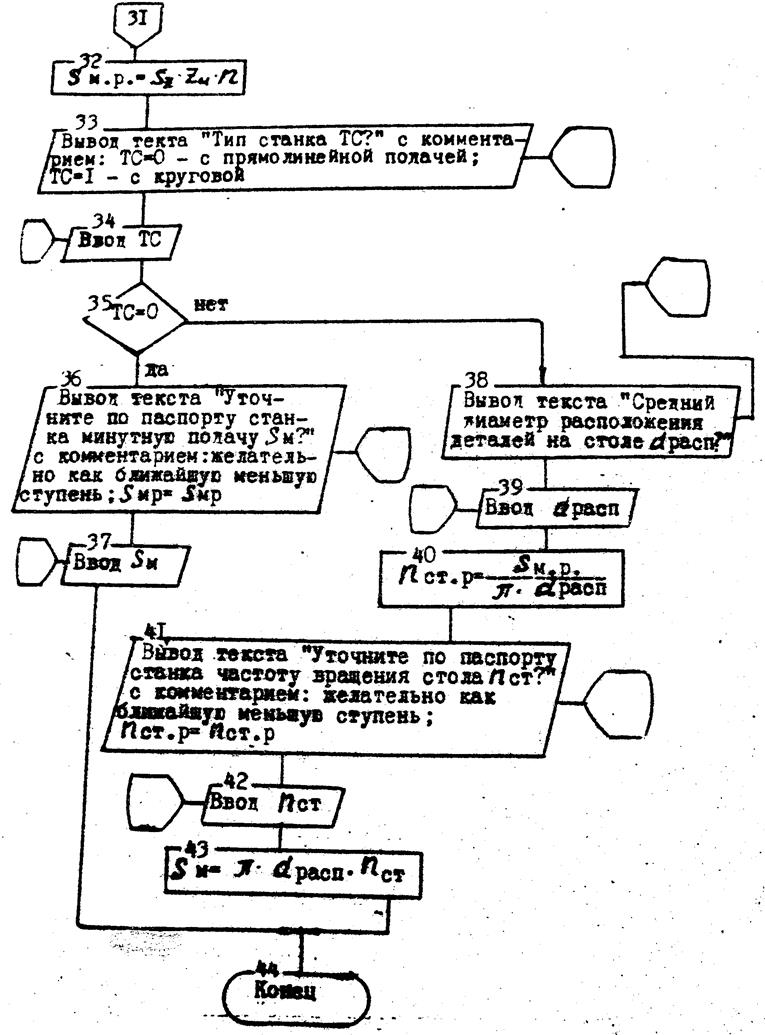
Рисунок 3.5 Схема алгоритма, реализующая блок 5 (Рисунок 3.1)

продолжение

Математическая модель для блока 6 и 7 рисунок 3.1 может   бить представлена следующими зависимостями:

- основное машинное время обработки tм в мин

,

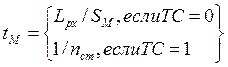- фактическая величина подачи на зуб фрезы Sz мм/зуб (по принятым режимам резания)   

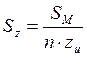, если ТС=0

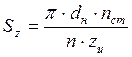, если TC=1

где - наибольший диаметр расположения деталей на столе станка.

Данный фрагмент математической модели может быть представлен схемой алгоритма, изображенной на рисунке. 3.6.

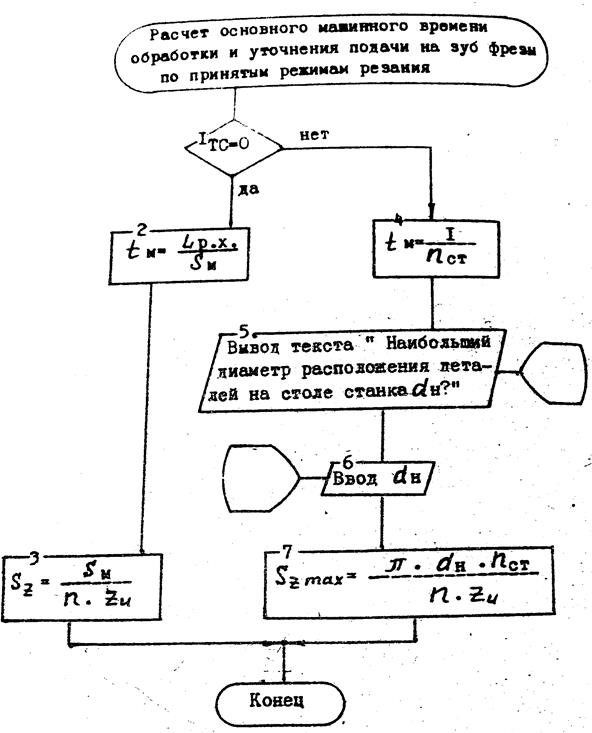
Рисунок 3.6 Схема алгоритма, реализующая блок 6 и 7 (Рисунок 3.1)

Математическая модель для блока 8 рисунок 3.1 может быть представлена следующими эмпирическими зависимостями и нормативными материалами

-  Потребная мощность Nр в кВт определяется по карте Ф-5 [5], представленной на стр.101 – 103

- для торцовых и дисковых двусторонних фрез

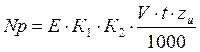
- для дисковых трехсторонних. Цилиндрических, концевых, радиусных, прорезных и угловых фрез

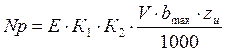
где Е – величина, определяемая по таблице (стр.102 [5]);

V - скорость резания в м/мин;

t - глубина резания в мм;

 - максимальная ширина резания в мм;

К1 – коэффициент, зависящий от обрабатываемого материала и определяется по таблице (с.103[5]);

К2 – коэффициент, зависящий от типа фрезы и определяется по таблице (с.103[5]);

Представленные две последние формулы отличается друг от друга только сомножителями t и bmax. Поэтому введя новое имя переменной, например, С, получим одну зависимость

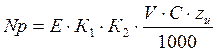
в которой для первой группы фрез С=t, а для второй С=bmax.

Учитывая, что для определения Е в таблице большое количество значений, а также требуется программным путем найти значение Е, то целесообразно данную таблицу аппроксимировать эмпирической зависимостью

.

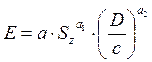При этом получим всего по четыре значения параметров a, a₁и а₂ зависимости от обрабатываемого материала и типа фрезы. Значения этих параметров надо определить до использования общей зависимости

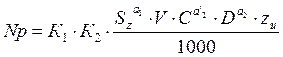
где а’₂=1-а₂.

Значения K₁ и K₂ будем определять по второму варианту подхода к расчету значений  K₁ и К₂.

-  Проверка по мощности двигателя  N_дв

, где η - к.п.д. станка (величины η и Nдв задаются как исходные данные).