Система стабилизации продольного движения летательного аппарата

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА 12

КУРСОВАЯ РАБОТА (ПРОЕКТ)
ЗАЩИЩЕНА С ОЦЕНКОЙ

РУКОВОДИТЕЛЬ

				А.И. Панфёров
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ

СИСТЕМА СТАБИЛИЗАЦИИ ПРОДОЛЬНОГО ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА

по дисциплине: СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЛА

РАБОТУ ВЫПОЛНИЛ(А)

СТУДЕНТ ГР.	1321				С.Д. Евстафьев
			подпись, дата		инициалы, фамилия

Санкт-Петербург
2008

СОДЕРЖАНИЕ

УРАВНЕНИЯ ДВИЖЕНИ ЛА. ОСНОВНЫЕ ПФ…………………………………………..3

СИНТЕЗ РУЛЕВОГО ПРИВОДА………………………………………………………….....7

Синтез оптимальной системы стабилизации………………………………8

СИНТЕЗ ФИЛЬТРА КАЛМАНА ДЛЯ СИСТЕМЫ СТАБИЛИЗАЦИИ ТАНГАЖА……12

ВЫВОДЫ………………………………………………………………………………………18

Приложение 1…………………………………………………………………………………19

СПИСОК ЛИТЕРАТУРЫ…………………………………………………………………….21

УРАВНЕНИЯ ДВИЖЕНИ ЛА. ОСНОВНЫЕ ПФ.

Существуют различные методы синтез систем управления. В данном курсовом проекте рассматривается проектирование СУ в частотной области. Исходными данными для синтеза являются передаточные функции и частотные характеристики. Рассмотрим для примера средний поршневой самолет, летящий со скоростью 80 м/с на высоте 1 км. Уравнения движения ЛА имеют вид:

,

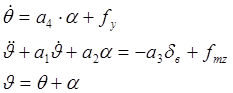где  и  - возмущающие силы вдоль соответствующих осей;

 - соответственно углы тангажа, наклона траектории и атаки;

 - отклонение руля высоты (управляющее воздействие);

 - характеризует аэродинамическое демпфирование ЛА в продольной плоскости;

 - характеризует устойчивость ЛА по углу атаки или перегрузке;

 - характеризует эффективность руля высоты;

 - характеризует свойство управляемости ЛА.

            Основные передаточные функции ЛА:

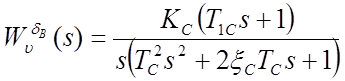
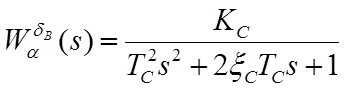
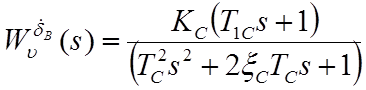
где

;    ;

;   .

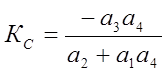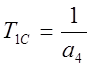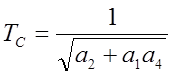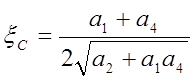Все эти коэффициенты считаются в программе, написанной в MatLab, текст которой приведён в Приложении1.

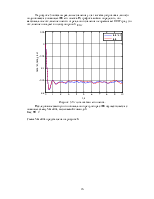
Ниже на рисунках 1 - 3 приведены переходные процессы некоторых ПФ, из них следует, что ЛА устойчив.

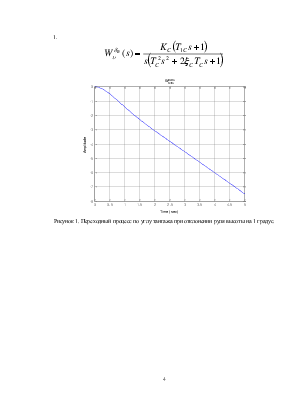
1.

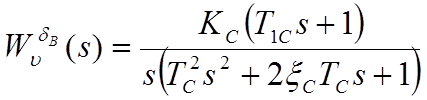
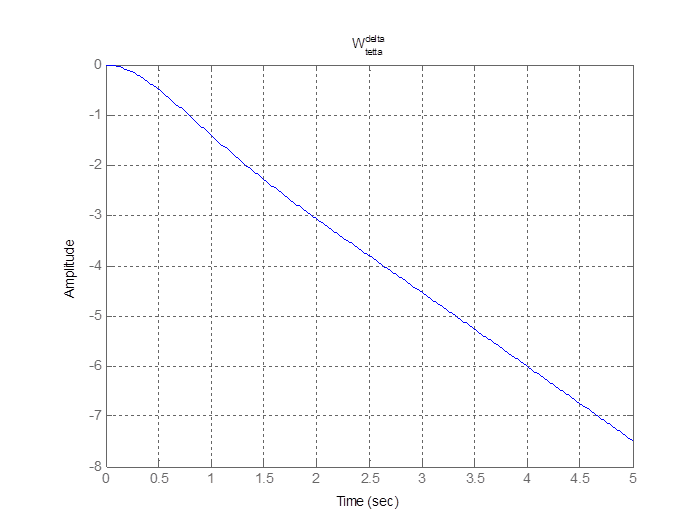
Рисунок 1. Переходный процесс по углу тангажа при отклонении руля высоты на 1 градус.

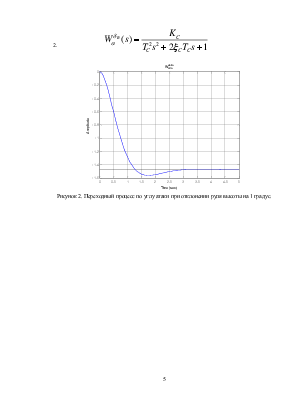
2.                            

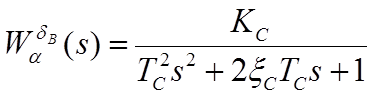
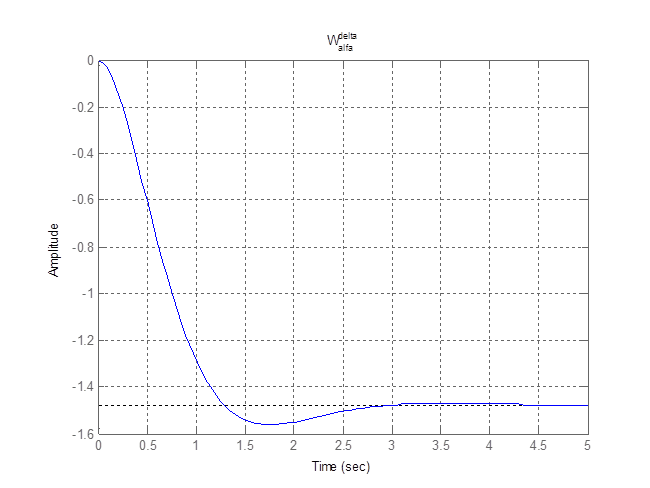
Рисунок 2. Переходный процесс по углу атаки при отклонении руля высоты на 1 градус.

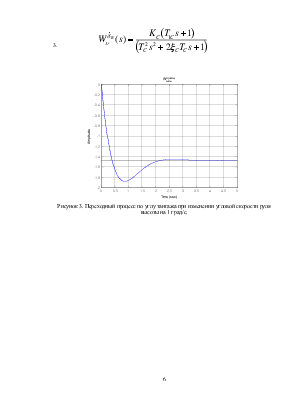
3.                           

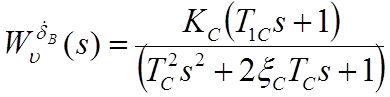
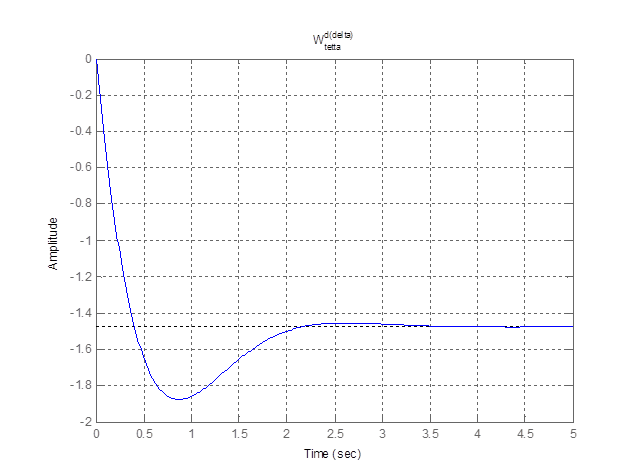
Рисунок 3. Переходный процесс по углу тангажа при изменении угловой скорости руля высоты на 1 град/с.

СИНТЕЗ РУЛЕВОГО ПРИВОДА

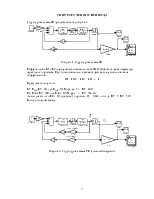
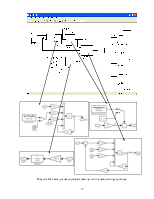
Структурная схема РП представлена на рисунке 1.

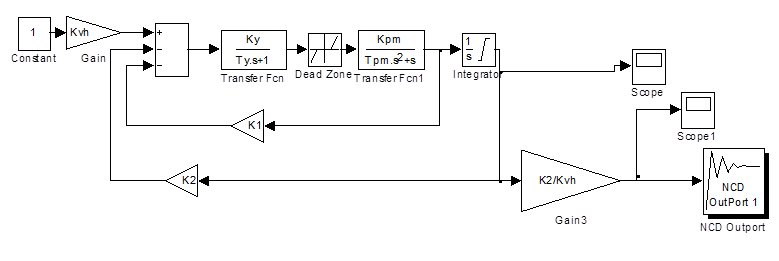
Рисунок 4. Структурная схема РП.

Коэффициенты К1 и К2 определяем с помощью блока NCD Outport, задавая параметры переходного процесса. При этом изначально в схеме задаются следующие значения коэффициентов:

В результате получили:

К1=К_ГОС·К1’=36, где К_ГОС=0,1 В/град/с   =>   K1’=360

К2=К_ЖОС·К2’=480, где К_ЖОС=0,9 В/град  =>   K2’=533,33

А если учесть, что  К_РМ=0,5 град/с/мА и принять , то тогда  K1’=1, K2’=1,48.

В итоге получим схему:

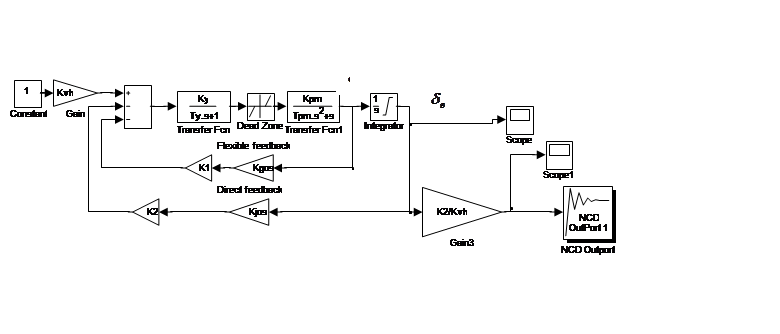
Рисунок 5. Структурная схема РП (конечный вариант).

Синтез оптимальной системы стабилизации

1.  Запишем уравнения ЛА в виде.

;

.

1.1.  Исходные уравнения имеют вид:

;

.

Обозначим , , получим

;

;

.

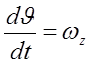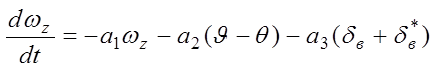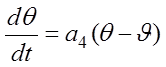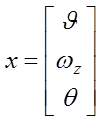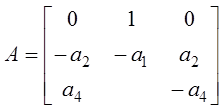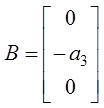;   ;   ;   ;   B₁= B. 

1.2.  Выбор матриц C и D определяется (На этапе синтеза системы стабилизации!) переменными, графики которых необходимо анализировать. Если представляют интерес графики и, тогда

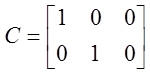;    D=0.

2.  Зададим матрицы весовых коэффициентов функционала

,

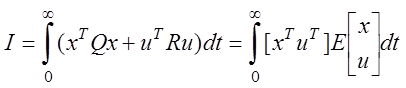где ; ;      ;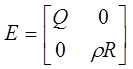

,  ;           ,      ;, ;      ,    .

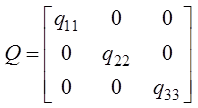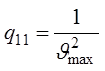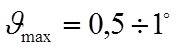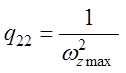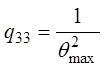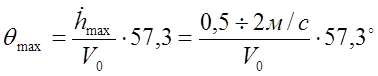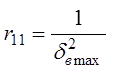3.  Вычислить матрицу коэффициентов передачи оптимального закона управления k

u (t) = -Kx(t).

Или для данного случая

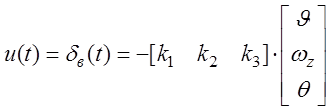
В программе матрица k вычисляется с помощью команды

> K = lqr(A,B,Q,R)

K =

   -0.8837   -0.8864   -0.5305

4.  Замкнуть систему. Уравнения замкнутой системы.

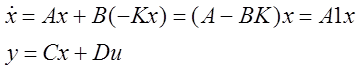
Вычислим матрицу A1

> A1=A-B*K;

5.  При синтезе системы стабилизации тангажа важным параметром является . По заданию , где  определяется типом РМ.

5.1.  Покажем сначала, как построить график производных вектора выхода

Пусть уравнение объекта имеет вид

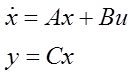, D=0.

Дифференцируя уравнение измерений и учитывая первое уравнение, получим:

.

Введем новый вектор выхода , тогда:

              

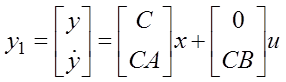
или

,

где  ,.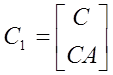

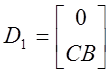
5.2.  Используем полученный результат для построения .

Для оптимального ЗУ:

,                      .

Организуем вектор выхода:

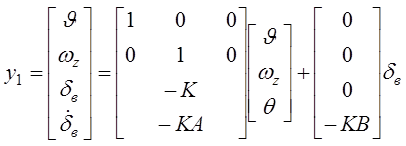
или

,

где  ,  .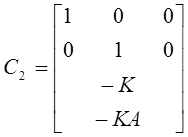

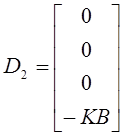Компоновка замкнутой системы управления

> sys=ss(a1,b1,c2,d2);

Корректируя матрицы Q и R сформируем оптимальную систему стабилизации. Для этого будем менять в программе значения следующих переменных , , , , пределы значений которых указаны выше. Построим переходные процессы для выходного вектора  при действии единичного возмущения. При этом необходимо определить время регулирования ; максимальное значение  и . Сравнить их с допустимыми значениями  . Определить  и сравнить с .

Результаты корректировки матриц сведены в таблицу 1.

Таблица 1.