Система стабилизации продольного движения летательного аппарата, страница 3

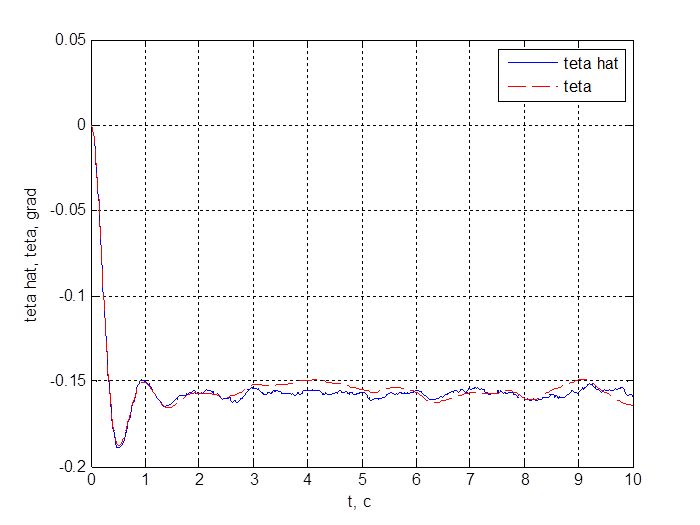
Рисунок 5. Угол тангажа и его оценка.

Исследование замкнутого оптимального регулятора с ФК осуществляется с помощью схему Simulink, вызываемой командой

Reg_FK_2

Схема Simulink представлена на рисунке 6

 

 

 

 

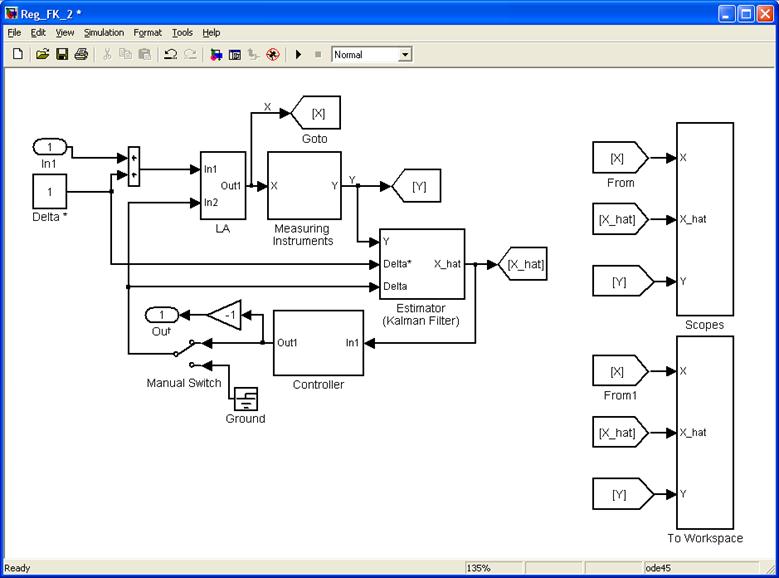
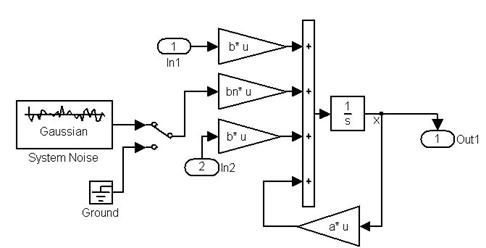
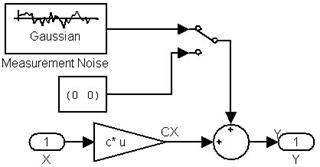
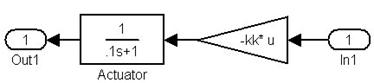
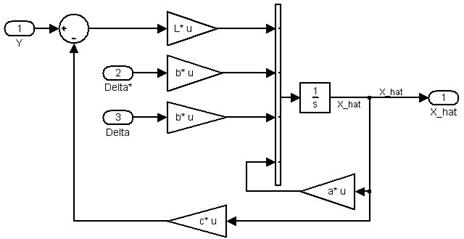
Рисунок 6. Схема для исследования замкнутого оптимального регулятора.

ВЫВОДЫ

        В курсовой работе разработана система стабилизации тангажа для среднепоршневого самолёта, летящего на высоте 1 км со скоростью 80 м/с, с использованием алгоритма фильтра Калмана. В результате был получен оптимальный закон управления. При таком законе управления время регулирования угла тангажа составило 1,14 сек, максимальное значение угловой скорости тангажа и угловой скорости руля высоты сотставили соответственно 0,414 и 6,94 град/с, что не превышает предельно допустимых значний. Статическая ошибка угла тангажа составила 0.157 град., что также не превышает допустимого значения. Для реализации оптимального закона управления руля высоты необходимо непрерывно измерять все компоненты вектора состояния ,и . Для измерения  и  используют гироскопические приборы, а измерение угла наклона траектории  представляет известные трудности. Для решения этой проблемы и используется ФК, который позволяет восстановить весь вектор состояния по неполным измерениям. В установившемся режиме точность оценок вектора состояния определяется следующими значениями:

, , .

Время готовности ФК составило . Оценки измерений получились достаточно точными, например, для угла тангажа максимальное отклонение оценки от истинного значения составило не более 0,007 град. Такое сравнение конечно же возможно только в рамках модели.

Приложение 1.

clear all; close all; clc;

%% исходные данные

a1 = 1.65;  % [1/c] хар-ет аэродин. демпфир-е ЛА в продольной пл-ти

a2 = 3.23;  % [1/c^2] хар-ет уст-ть ЛА по углу атаки или перегрузке

a4 = 1.61;  % [1/c] хар-ет св-во управляемости ЛА

a3 = 5.4;   % [1/c^2] хар-ет эффективность руля высоты

v = 80;     % [м/с]

H = 1;      % [км]

Ty = 0.01;  % [c] постоянная времени усилителя

Tpm = 0.015;% [c] постоянная времени РМ

Ky = 720    % [мА/В] коэф-т усиления усилителя

Kpm = 0.5   % [(град/с)/мА]

K1 = 1      %

K2 = 1.48   %

Kvh = 5     %

Kgos = 0.1  % [В/(град/с)] ГОС

Kjos = 0.9  % [В/град] ЖОС

L = 200;  % [м] масштаб турбулентности

% конструктивные

h_dot_max= 2        % [м/с] вертикальная скорость

tetta_max = 0.5;      % [град]

omega_max = 5;      % [град/с]

Tetta_max =h_dot_max*57.3/v;      % [град]

delta_h_max = 3;    % [град]

% статистические

sigmaW = 2;          % [м/с] среднеквадратическое значение скорости ветра

sigmatetta = 0.1;      % [град]

sigmaomega = 0.1;     % [град/c]

Tf = 0.1;            % [1/c^2]

%% вычисление коэффициентов

Tc=(a1*a4+a2)^-0.5                 % [с] опред-ет быстроту реакции ЛА на отклонение руля

ksi_c=0.5*(a1+a4)*(a1*a4+a2)^-0.5  % чем больше устойчивость, тем меньше ksi_c

T1c=1/a4                           % [c] хар-ет запаздывание между поворота корпуса ЛА и искривлением траектории

Kc=-a3*a4/(a1*a4+a2)               % []

K1c=a4/(a1*a4+a2)                  %  []

%% Схема РП

shema1

sim('shema1')

%% графики преходных процессов

W_alfa_delta=tf([Kc],[Tc^2 2*ksi_c*Tc 1])

figure

step(W_alfa_delta,5)

title('W_a_l_f_a^d^e^l^t^a')

grid on

figure

W_tetta_delta=tf([Kc*T1c Kc],[Tc^2 2*ksi_c*Tc 1 0])

step(W_tetta_delta,5)

title('W_t_e_t_t_a^d^e^l^t^a')

grid on

figure

impulse(W_tetta_delta,5)

title('W_t_e_t_t_a^d^(^d^e^l^t^a^)')

grid on

%% Синтез оптимальной системы стабилизации

% Матрицы ЛА

A = [0 1 0; -a2 -a1 a2; a4 0 -a4];

B = [0; -a3; 0];

B1 = [0; -a3; 0]*3;   % b*delta maximum

C = [1 0 0; 0 1 0];

D = 0;

% Матрицы весовых коэф-тов функционала

q_tetta = 1/tetta_max^2; q_omega = 1/omega_max^2; q_Tetta = 1/Tetta_max^2;

r_delta_h = 1/delta_h_max^2;

Q = [q_tetta  0 0;0 q_omega 0;0 0 q_Tetta]

R = r_delta_h

% Синтез регулятора

K = lqr(A,B,Q,R)     % Вычисление матрицы коэффициентов передачи оптимального закона управления

A1=A-B*K;            % замыкаем систему

C1 = [C;-K];         % выходной вектор с delta

C2 = [C1;-K*A1]     % выходной вектор с delta_dot

D2 = [0;0;0;-K*B];   % выходной вектор с delta_dot

sys=ss(A1,B,C2,D2); % Компоновка замкнутой системы управления

figure

step(sys,5);        % Построение переходных процессов для интервала времени от 0 до 5 с

hold on;

ltiview(sys);        % Вызов программы ltiview для анализа замкнутой системы во временной и частотной областях

grid on

%%  Фильтр Калмана

%  Ввод матриц объекта управления для расчета фильтра Калмана:

An=A;  Bn=[0; -a2; 0];  Cn= C;  Dn=D;

%  Ввод интенсивностей шумов:

Qn = [2*sigmaW*sigmaW*L/v^3]

rn11 = [2*sigmatetta*sigmatetta*Tf];

rn22 = [2*sigmaomega*sigmaomega*Tf];

%  Формирование матрицы интенсивностей ошибок измерителей

Rn = [rn11 0; 0 rn22]

%  Формирование объекта для синтеза ФК

sysn=ss(An,Bn,Cn,Dn)

%  Расчет ФК

[kest,L P] = kalman(sysn,Qn,Rn)

%  Вычисление собственных чисел (корней характеристического уравнения ФК)

eig(kest)

%  Анализ процеесов и построение частотных характеристик ФК

ltiview(kest)

%  Исследование замкнутого оптимального регулятора с ФК

Reg_FK_2

sim('Reg_FK_2')

figure

plot(tout,teta_hat)

grid on

hold on

plot(tout,teta,'r--')

hold off

СПИСОК ЛИТЕРАТУРЫ

1. Хованский Ю. М., Пономарев В.К. Стабилизация летательных аппаратов , 1979.

Задание на курсовое проектирование системы стабилизации продольного движения ЛА по курсу: Системы автоматического управления ЛА.

Вариант №17

Параметр	Значение
Тип ЛА	Средний поршневой самолет (СПС)
a1, с-1	1,65
a2, с-2	3,23
a3, с-2	5,4
a4, с-1	1,61
a5, с-1	-
v, м/с	80
H, км	1