Система стабилизации продольного движения летательного аппарата, страница 2

	1	0.5	0.5	0.5	0.5	1	0.5	0.5
	1	1	1	3	5	1	5	5
	1	1	1	1	1	1	0.5	2
	1	1	2	2	3	3	3	3
	1.97	1.24	1.3	1.25	1.43	1.4	1.23	1.14
	-0.62	-0.55	-0.34	-0.48	-0.4	-0.26	-0.38	-0.414
	-4.94	-5.51	-11.1	-5.92	-7.13	-15.8	-7.71	-6.94
,	-0.58	-0.41	-0.21	-0.21	-0.14	-0.19	-0.1	-0.157

Из всех приведённых вариантов выбираем последний, т.к. при данных значениях элементов матриц Q и R время регулирования  минимально и остальные параметры переходных процессов удовлетворяют требованиям. Переходные процессы для выходного вектора  представлены на рисунке 1.

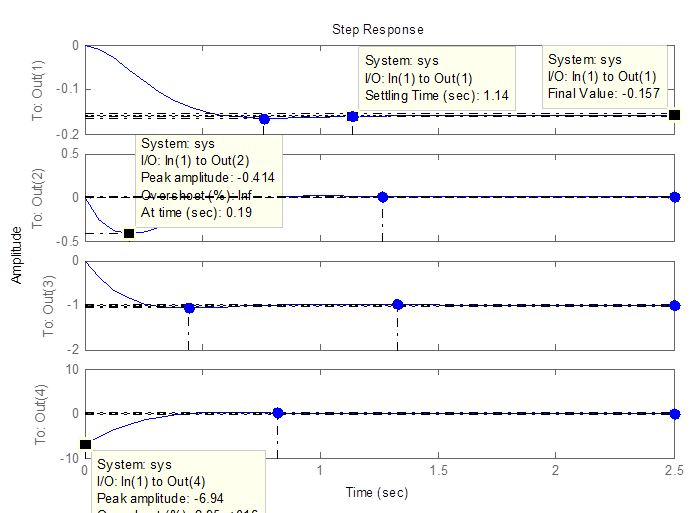
Рисунок 3. Переходные процессы для выходного вектора .

СИНТЕЗ ФИЛЬТРА КАЛМАНА ДЛЯ СИСТЕМЫ СТАБИЛИЗАЦИИ ТАНГАЖА.

1.  Постановка задачи.

Для реализации оптимального закона управления руля высоты

необходимо непрерывно измерять все компоненты вектора состояния ,и . Для измерения  и  используют гироскопические приборы, а измерение угла наклона траектории  представляет известные трудности. . Поставим задачу в двух вариантах:

-по измерению ;

-по измерению  и .

Необходимо восстановить весь вектор состояния.

Такая задача в любой из приведенных постановок может быть решена использованием алгоритма фильтра Калмана (ФК). В достаточно общей постановке задача синтеза ФК формулируется следующим образом.

Для данных уравнений объекта, возбуждаемого белым шумом

и уравнений измерений, содержащих аддитивную ошибку типа белого шума

,

где ,           ;

, .

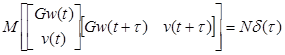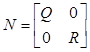Здесь M – математическое ожидание.

Получить оценку  вектора состояния , минимизирующую ошибку

.

Приведем математическую модель летательного аппарата (ЛА) и измерений к требуемому виду. Для этого необходимо учесть случайные возмущения, действующие на ЛА и ошибки измерителей.

2.  Математическая модель объекта управления.

Уравнения ЛА при учете составляющей турбулентности нормальной к траектории имеют вид     [Хованский Ю. М., Пономарев В.К. Стабилизация летательных аппаратов , 1979].

;

или в векторной форме:

,

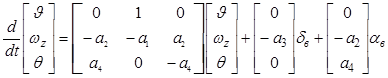где 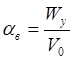;  - нормальная к траектории турбулентность атмосферы.

Обычно турбулентность атмосферы моделируют с помощью формирующих фильтров первого порядка:

.

где 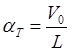, L –масштаб турбулентности ();

 -среднеквадратическое значение скорости ветра ( для средней турбулентности).

Для формирующего фильтра первого порядка корреляционная функция имеет вид:

,

а спектральная плотность:

.

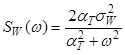Вернемся к уравнениям ЛА в векторной форме. Вектор случайных внешних воздействий можно записать следующим образом:

.

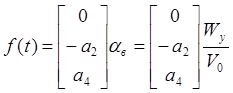Матрицу корреляционных функций для этого вектора при замене  эквивалентным белым шумом как показано выше получим так

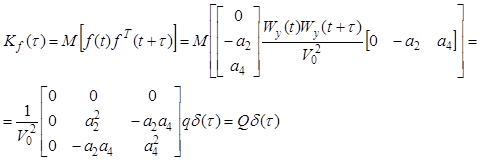
Здесь.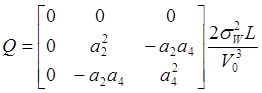

3.  Математическая модель измерителей.

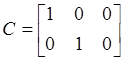Пусть измеряются и , тогда матрица , а вектор ;

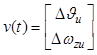 и  -широкополосные случайные ошибки соответствующих гироскопических измерителей, моделируемые, как правило, уравнениями первого порядка. Корреляционные функции эквивалентных белых шумов , , 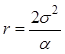где 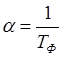  -среднеквадратическая ошибка и постоянная, обратная постоянной времени фильтра прибора (). , .

Корреляционная функция ошибок измерителей в этом случае имеет вид:

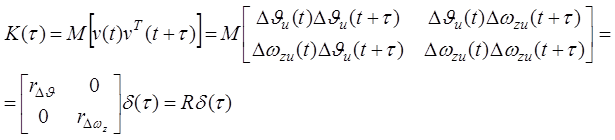
Здесь обозначено

;    ; ;

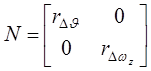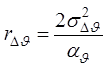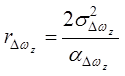4.  Если измеряется только , то , , .

5.  Уравнения фильтра Калмана.

Уравнение фильтра Калмана для установившегося состояния имеют вид:

, где матрица коэффициентов передачи ,а Р является единственным положительно-определенным решением алгебраического уравнения Риккати:

.

Матрица Р это матрица ковариаций ошибки оценки вектора состояния, т.е.

   при

Диагональные элементы этой матрицы являются дисперсиями ошибок оценок соответствующих компонент вектора состояния и служат для определения точности оценок в установившемся состоянии.

6.  Расчет фильтра Калмана на ЭВМ

Ввод матриц объекта управления для расчета фильтра Калмана:

an=a; bn=[0; -a2; a4]; cn= c; dn=d;

Ввод интенсивностей шумов

qn = [2*sigmaW*sigmaW*L/V0^3]

rn11 = [2*sigmateta*sigmateta*Tf];

rn22 = [2*sigmaomega*sigmaomega*Tf];

Формирование матрицы интенсивностей ошибок измерителей

rn = [rn11 0; 0 rn22]

Формирование объекта для синтеза ФК

sysn = ss(an,bn,cn,dn)

Расчет ФК

[kest, L, P] = kalman(sysn,qn,rn)

Результатом выполнения команды kalman являются 3 объекта: kest, L, P. Первый объект kest содержит информацию о фильтре Калмана в виде

     , 

     

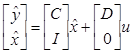
Второй и третий объекты это матрица коэффициентов передачи ФК L и матрица ковариаций ошибки оценки вектора состояния P:

L =

    0.7569    0.3465

    0.3465    2.4470

    0.5200    0.0186

P =

    0.0015    0.0007    0.0010

    0.0007    0.0049    0.0000

    0.0010    0.0000    0.0009

            Диагональные элементы матрицы Р являются дисперсиями ошибок оценок соответствующих компонент вектора состояния и служат для определения точности оценок в установившемся режиме:

, , .

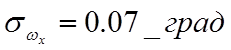Можно также определить 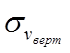, так как 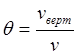, то, зная , находим:

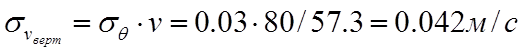
Вычисление собственных чисел (корней характеристического уравнения ФК)

eig(kest)=

  -0.7009         

  -2.8815 + 0.9852i

  -2.8815 - 0.9852i

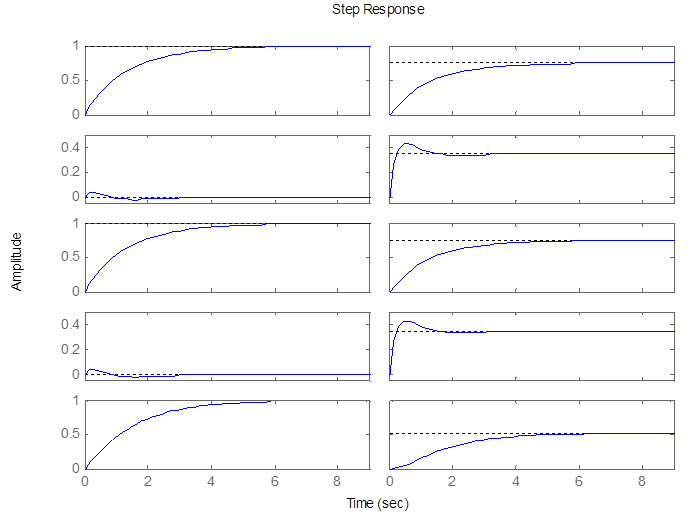
Анализ процессов и построение частотных характеристик ФК. С помощью команды ltiview(kest) построим переходные характеристики (Рисунок 4). По полученным характеристикам определяем время готовности ФК, оно равно

                                                                                   

Рисунок 4. Временные характеристики ФК.

На рисунке 5 показаны реальные значения угла тангажа (штриховая линия) и получившаяся с помощью ФК его оценка. Из графика можно определить, что максимальное отклонение оценки от реального значения не превышает 0.007 град, это отклонение попадает в полосу шириной .