Расчет движения динамической модели наземного буксируемого артиллерийского орудия

 РАСЧЕТ ДВИЖЕНИЯ ДИНАМИЧЕСКОЙ МОДЕЛИ 

НАЗЕМНОГО БУКСИРУЕМОГО  АРТИЛЛЕРИЙСКОГО ОРУДИЯ  

1. Последовательность действий при использовании уравнений Лагранжа II рода для решения задач о движении голономных систем

2..Описание модели наземного буксируемого артиллерийского орудия

3. Выбор обобщенных координат..  3.3 Расчет кинетической энергии системы.

4 Уравнения Лагранжа второго рода для данной системы

5 Виртуальная работа сил, действующих на рассматриваемую систему.

Обобщенные силы..

6.Уравнения Лагранжа второго рода в матричной форме

1.Последовательность действий при использовании уравнений Лагранжа II рода для решения задач о движении голономных систем

1.Определить число степеней свободы системы и выбрать наиболее удобные обобщенные координаты.

2. Вычислить кинетическую энергию системы в ее абсолютном движении и выразить эту энергию через обобщенные координаты  и обобщенные скорости .

 Формулы  кинетических энергий в абсолютном движении:

·  для материальной точки ;

·  для системы материальных точек  ;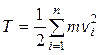

·  для твердого тела:

– при поступательном движении  ;

– при вращении вокруг неподвижной оси  l;

– при плоскопараллельном движении

;

– при вращении вокруг неподвижной точки ;

– в общем случае движения твердого тела

.

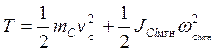3. Вычислить производные от кинетической энергии, входящие в левую часть уравнений Лагранжа.

4. Определить обобщенные силы, соответствующие выбранным обобщенным координатам (так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты).

5. Подставить все вычисленные величины в уравнения Лагранжа.

2.Описание модели наземного буксируемого артиллерийского орудия

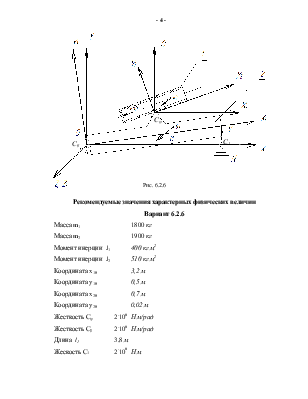
В данной работе не рассматриваются реальные конструкции образцов вооружения непосредственно, поскольку в виду сложности  математическое описание их движения традиционными методами наталкивается на большие трудности. Поэтому в работе описание явлений осуществляется на уровне упрощенных динамических моделей  объектов вооружения конкретных конструктивно-компоновочных схем. Например, вместо пространственной, четырехмассовой  механической системы с 14 степенями свободы (рис. 1.1, 1.2) в качестве математической модели наземного буксируемого артиллерийского орудия при выстреле  принята двухмассовая, плоская (в плоскости симметрии орудия при нулевом угле горизонтального обстрела) система с 2-мя степенями свободы. Сила давления пороховых газов на дно канала ствола (цилиндра 3) зависит от переменной нагрузки Р(t), рассчитываемой по формуле (4.2).

3.Описание модели наземного буксируемого артиллерийского орудия

Рис.6.2схема 6

Полый цилиндр 2 массой m2 может вращаться вокруг оси O3Z3 шарнира, закрепленного на основании 1 массой m1.  Основание закреплено в цилиндрическом шарнире О и опирается на вертикальную пружину  KN с жесткостью C₁. Вращение цилиндра относительно основания сдерживается спиральной пружиной с крутильной жескостью С_j, а вращение основания относительно фундамента – спиральной пружиной с крутильной жесткостью С_θ.В шарнирах О и О₃ построены системы координат OXYZ и O₃X₃Y₃Z₃, оси OX и O₃X₃ которых горизонтальны, неизменно  связаны с цилиндром и основанием. Расстояние от точки  O₃ до оси цилиндра h=0,06 м. Размеры системы задаются, во-первых, координатами x_3O=3,3 м, y_3O=0,5 м центра масс основания 1 в системе координат OX₁Y₁Z₁. Длина основания OK равна l₁.  Начальное положение системы задается углом θ₀ между осью OX₁ и горизонталью и углом j₀ между осью O₃X₂ и горизонталью. Моменты инерции основания и цилиндра относительно осей O₁z₁ и O₂z₂ равны J₁ и J₂ соответственно. Спиральная пружина в шарнире О в начальном положении не деформирована. При этом пружина в шарнире О₃ и вертикальная пружина  KN поддерживают систему в положении равновесия.

 В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P(t), определяемая по формуле (6.1). При этом цилиндр начинае вращаться вокруг оси O₃Z₃, а основание – вокруг оси OZ₁.

  Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.