Теоретические основы проектирования уравновешивающих механизмов

Теоретические основы проектирования уравновешивающих механизмов

Исходными данными при проектировании УМ являются (рис.1.6.):

1. Параметры КЧ орудия:

Q_K   -   масса КЧ;

c_{K     -}   расстояние методу осью цапф и центром тяжести КЧ;

r    -   расстояние от оси цапф до подвижного шарнира;

a    -  расстояние от оси цапф до неподвижного шарнира;

φ_max  -  max угол возвышения КЧ;

φ_{min   -}   min угол возвышения КЧ;

β    -   угол между радиусами a и r;

  - угол между горизонтом и линией, соединяющей центр оси цапф и центр тяжести качающейся части;

2. Либо вместо a,r и  β  задаются координаты опорных точек УМ:

Xа,Yа  - координаты подвижного шарнира (А);

Xb,Yb  - координаты неподвижного шарнира (В).

Вынос центра тяжести качающихся частей вперед к  дульному срезу относительно оси цапф создает момент силы тяжести Мк качающейся части АО, определяемый по зависимости

,                                                  где     .

,                                                                                         

Знаки ± в формуле (2) определяются конструкцией АО: если центр оси цапф, измеряя относительно оси ствола, находится выше центра тяжести качающейся части, то ставится знак «минус», если ниже – то «плюс».

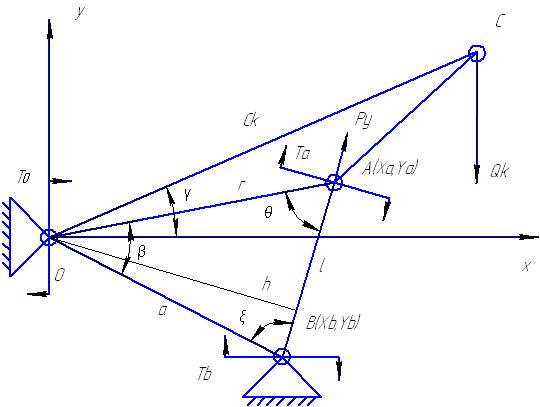
Рис 1. 1. Схема действия сил и моментов

Для компенсации действия этого момента введем момент уравновешивания вида:

,                                                                                     

где P_YM- сила уравновешивающего механизма;

h - плечо этой силы относительно оси цапф.

В результате в общем случае создается момент неуравновешенности качающейся части АО. Выбором типа уравновешивающего механизма (УМ) и его характеристик этот момент устраняется полностью или частично.

Для определения плеча УМ рассмотрим мнимый треугольник АОВ (рис.1.6). Параметры треугольника:

  

Параметр  определяется по теореме «косинусов»

.

Площадь треугольника:

    или по теореме «синусов»

.

Откуда, .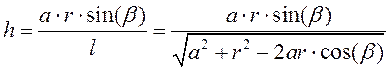

Тогда, момент создаваемый УМ определяется в виде:

Практический расчет начальных параметров   уравновешивающего механизма

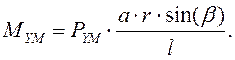
Моменты веса качающейся части и создаваемый УМ зависят от угла возвышения, т.к в них входят тригонометрические функции углов 

где  , - конструктивные углы соответствующие углу возвышения .

Выберем в качестве исходного .

Расчет параметров проводим в следующей последовательности:                   Расчет постоянных параметров

1. Определяем расстояние от оси цапф до подвижного шарнира:

.                                                                                  (4)

2.Определяем расстояние от оси цапф до неподвижного шарнира

.                                                                        (5)

3. Находим угол между размерами a и r при φ=0⁰

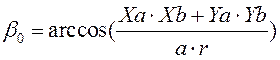.                                                   (6)

Расчет циклических параметров

Диапазон углов возвышения φ_min ... φ_max, представляем дискретным рядом с интервалом Δφ: φ_i = φ_i-1 + Δφ.

Все дальнейшие расчеты целесообразно свести в таблицу.^[1]

φi градус	φir радиан	αi=α0+ φi	βi=β0+ φi	li, м	λi, м	hi, м	Mki, Н •м	Gi, Н
φmin	φminr
0 . φi . .	0 . φir . .	α0	β0	l0	λ0	h0	Mk0	G0
φmax	φmaxr	αm	βm	lm	λm	hm	Mkm	Gm

При вычислениях используются следующие выражения:

·  расстояние l_i между неподвижными и подвижными шарнирами УМ, т. е. текущее расстояние АВ                                       

 ,

·  плечо  действия   силы   УМ  на   качающуюся часть орудия относительно оси цапф                                                 

,

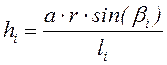·  ход  подвижного шарнира А относительно неподвижного В

 , где значение l_m = l_i  при ;

·  момент   веса   качающейся части для всего

,

·  значения силы веса качающейся части орудия, приведенной к зоне подвижного шарнира А

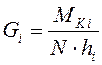, Н.