Расчет механизма клинового затвора

Кафедра Е1

Лабораторная работа

РАСЧЁТ МЕХАНИЗМА КЛИНОВОГО ЗАТВОРА

Выполнил: Иванов И.Н.

группа Е191

Проверил: Агошков О.Г.

Санкт-Петербург

2014

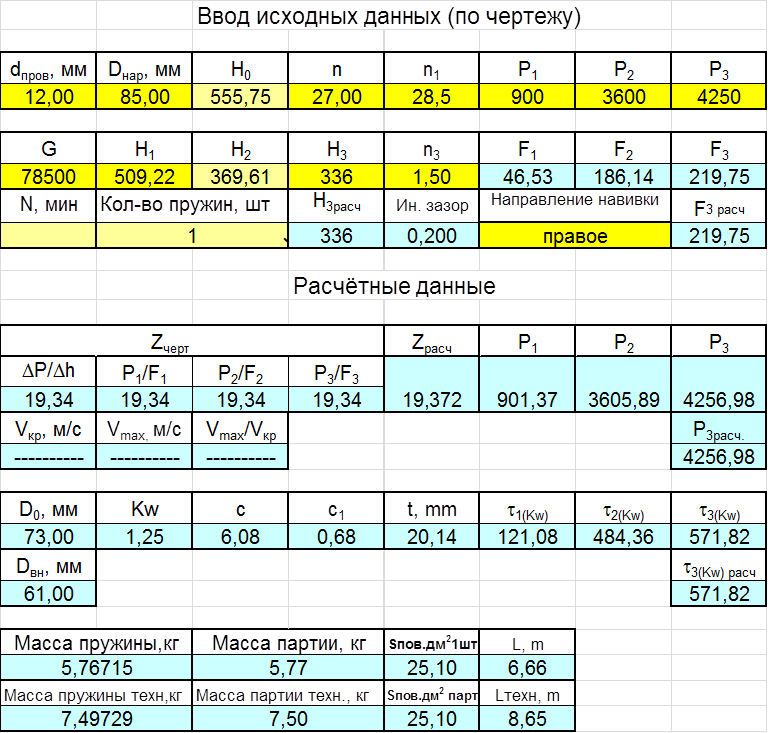
Расчет пружины:

Усилие предварительного поджатия принимаем:

; .

,

.

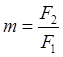Работа пружины:

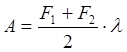, где - рабочий ход пружины.

.

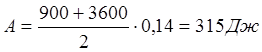Энергия затрачиваемая на подъем клина:

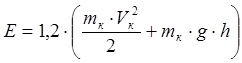, где -масса клина;

-скорость клина;

-высота подъема клина.

.

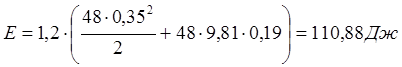Имея величину энергии , можно определить максимальную скорость, сообщаемую пружиной:

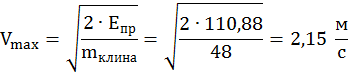
Жесткость пружины (в первом приближении):

;

.

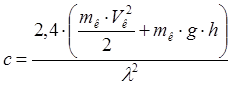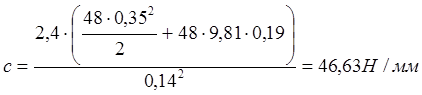жёсткость пружины:

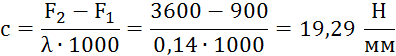
Жесткость одного витка:

.

Далее подбираем стандартную пружину.

По формуле (2) ГОСТ13768-86, пользуясь интервалом значений от 0,05 до 0,25 (формула (1) ГОСТ13765-86), находим граничные значения силы , а именно:

.

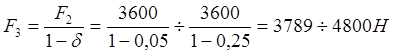В интервале от 3789Н до 4800Н в ГОСТ13768-86 пружин 1 класса, разряда 3 имеются следующие силы :  4000; 4250; 4500; 4750; 5000 Н.

Исходя из стремления обеспечить наибольшую критическую скорость, остановимся на витке со следующими данными (номер позиции 219):

      

Учитывая, что для пружин 1 класса норма напряжений  (ГОСТ13764-86), находим, что для найденного диаметра проволоки расчетное напряжение:

Принадлежность к 1 классу проверяем путем определения отношения , для чего предварительно определяем критическую скорость по формуле (5) ГОСТ13765-86:

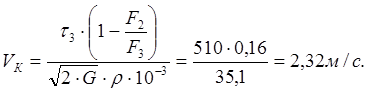
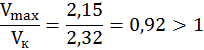
Полученная величина указывает на отсутствие соударения витков  и, следовательно, выбранная пружина удовлетворяет заданным условиям.

Далее определение остальных размеров производим по формулам табл.1 ГОСТ13765-86.

По формуле (6) находим жесткость пружины:

.

По формуле (7) определяем число рабочих витков пружины:

.

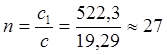Уточненная жесткость имеет значение:

.

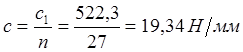При полутора нерабочих витках полное число витков находим по формуле (8):

.

По формуле (9) определяем средний диаметр пружины:

.

Предварительную, рабочую и максимальную деформации определяем по формулам (11), (12), (13):

;

;

.

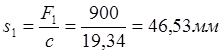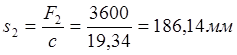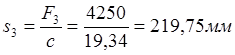Длину пружины при максимальной деформации, в свободном состоянии, при предварительной и рабочей деформациях вычисляем по формулам (14), (15), (16), (17):

;

;

;

.

Шаг пружины в свободном состоянии вычисляем по формуле (18):

.

Аналитическое решение:

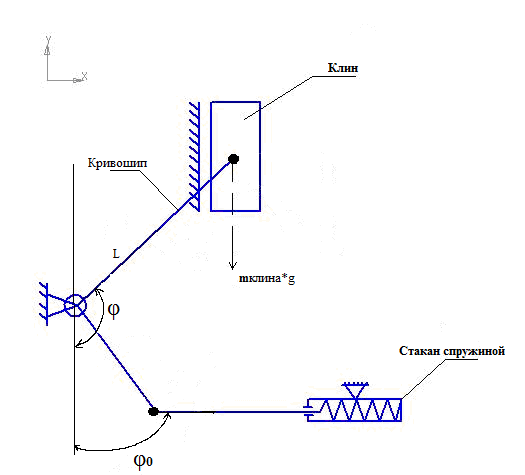
За обобщенную координату примем  – угол поворота кривошипа.

Тогда  – обобщенная скорость (угловая скорость).

Кинетическая энергия системы:

, где:

1) Кривошип (1) совершает вращательное движение вокруг точки М оси кривошипа.

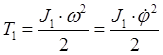 – кинетическая энергия кривошипа.

2) Клин (2) совершает поступательное движение.

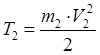– кинетическая энергия клина.

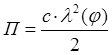 – потенциальная энергия пружины;

3) Скорость клина:

;

;

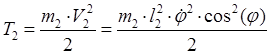4) 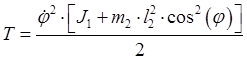 – кинетическая энергия системы, где – приведенный момент инерции.

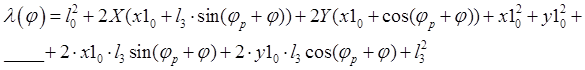 – рабочий ход пружины, как функция .

Уравнение Лагранжа второго рода:

.

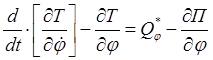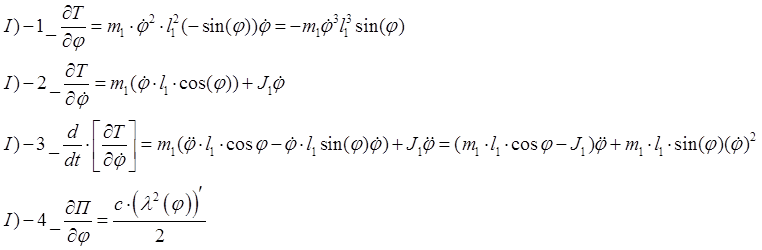
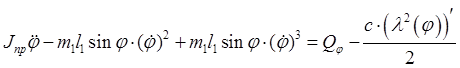
Определяем обобщённую силу :

Обобщённую силу необходимо определить в самом критическом случае, т.е. при максимальном угле возвышения .

В итоге выражение для обобщённой силы имеет вид:

Масса заряда определяется следующим образом:

Коэффициент трения в направляющих клина:

Коэффициент трения гильзы заряда:

Уравнение движения механизма клинового затвора запишем в виде:

Момент инерции кривошипа  рассчитываем как момент инерции консольной балки:

Масса кривошипа:

Плечо кривошипа:

Формируем начальные условия для решения уравнения:

Время:

Начальный угол поворота кривошипа:

Угловая скорость кривошипа:

Решение уравнения Лагранжа проведём при помощи пакета «MathCAD».

Необходимо обеспечить, чтобы за некоторый промежуток времени угол поворота кривошипа  достиг значения . Именно при этой конечной величине угла поворота кривошипа можно обеспечить требуемую высоту подъёма клина ().

В итоге получаем значения: