Язык математического моделирования динамических параметров систем был создан в 1998 году на кафедре Е1 БГТУ (Военмех).Автор - Гуц Д.В. Главный консультант - к.т.н., доцент Агошков О.Г.Необходимость создания такого языка появилась давно, но средства его реализации не отвечали поставленным требованиям. Только в недавнее время, благодаря внедрению в область научных исследований высокопроизводительной компьютерной техники, появилась возможность реализовать язык такого уровня. Проблема заключалось в необходимости разработки принципиально нового языка-интерпретатора в составе сложной вычислительной системы, что безусловно диктовало жесткие требования к быстродействию вычислительной системы, поскольку при численном интегрировании и дифференцировании производится значительный объем вычислений, особенно при многоточечных методах, повышающих точность.
Традиционно языки программирования делятся на два класса: компиляторы и интерпретаторы. Оба этих класса плохо подходят для решения задач моделирования. Традиционные языки-интерпретаторы (Basic,PL,Java,Perl) не обеспечивают достаточной скорости выполнения программы моделирования в составе основного программного модуля. Этот факт заставил отказаться от традиционных представлений и концепций программирования ради достижения необходимого быстродействия и точности вычислений. Языки-компиляторы вводят ограничения в программы исходя из заложенного в них алгоритма вычислений и для каждой новой задачи необходимо заново строить (компилировать) вычислительную программу.
В связи с вышеизложенными соображениями становится очевидна необходимость создания принципиально нового языка моделирования, объединяющего в себе гибкий алгоритм и высокую скорость вычислений по заданному изначально методу. интерпретатор программ "MDL" написан на языке "С". Этот модуль может присоединяться к любым, сколь угодно сложным, программам языков C, C++, Pascal, Fortran, Fort, Assembler и др. Наличие в расчетной системе внутреннего языка программирования позволяет отказаться от каких либо ограничений на спектр решаемых задач. иными словами, принципы расчета при различных классах задач остаются неизменными. Например, моделирование динамических параметров практически любой механических системы, с той или иной точностью, может быть осуществлено при использовании уравнений Лагранжа второго рода. Все задачи исследования можно свести к нескольким классам, исходя из необходимости применения определенных методов решения. Наличие в программе собственного, внутреннего языка программмирования позволяет:
- отказаться от жестких ограничений на спектр решаемых задач и тем самым расширить возможности вычислительной системы;
- повысить удобство использования вычислительной системы вцелом засчет отказа от множества идентификационных вопросов пользователю;
- вводить любые аналитические и таблично заданные функции в уравнения моделирования и выводить любые промежуточные функции;
- выводить любые промежуточные результаты расчета по желанию пользователя и вводить любые данные в процессе расчета;
- формировать базу данных решаемых задач с последующим обращением к ней для выявления общих закономерностей;
- подключать любые внешние исполняемые модули (.COM и .EXE).
Такие возможности являются недостижимыми для любой программы с жестко заданным алгоритмом. При использовании внутреннего языка программирования, в основной программе, пользователь сам формирует алгоритм вычислений. Неизменным остается лишь метод.
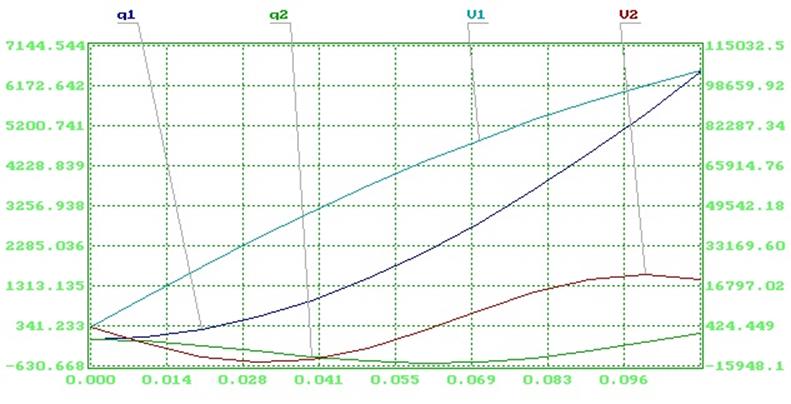
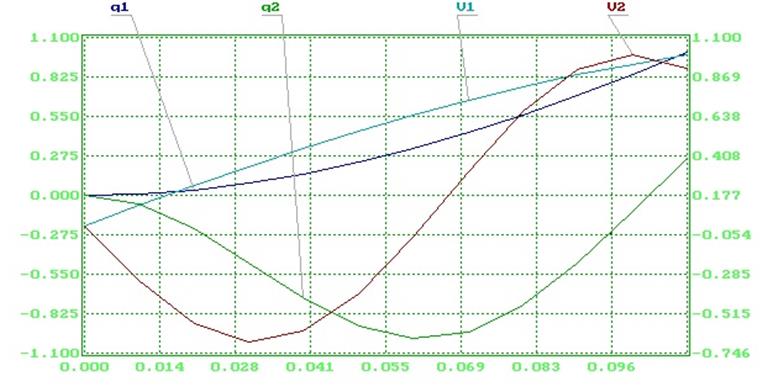
9. Файл данных для программы автоматического получения и интегрирования
уравнений Лагранжа. Результат расчета конкретного движения.
#DECLARE (t,tend,q[6],qt[6],Q[6],TKIN,EPOT,TU,FDIS);
#DECLARE (H,N,g,m1,m2,J1,J2,x10,y10,x20,y20,x30,y30,l,c);
#DECLARE (ce,cf,P1,a1,t1,P);
STATIC: t = 0.0;
tend = 0.1;
H = 0.01;
N = 2.0;
g = 9.8;
m1 = 1800.0;
m2 = 1900.0;
J1 = 400.0;
J2 = 5100.0;
x10 = 3.2;
y10 = 0.5;
x20 = 0.7;
y20 = 0.02;
x30 = 3.3;
y30 = 1.0;
l = 3.8;
c = 2000000.0;
ce = 2000000.0;
cf = 2000000.0;
P1 = 2.37E+10.0;
a1 = 6.68E+10.0;
t1 = 0.005;
q[1] = 0.0;
qt[1] = 0.0;
q[2] = 0.0;
qt[2] = 0.0;
DYNAMIC: P = P1-a1*(t-t1)*(t-t1);
Q[1] = P*(y20+y30)-0.5*c*l*l*sin(2*q[1])-ce*q[1]-m2*g*((x30*cos(q[1])-y30*sin(q[1]))+(x20*cos(q[2])-y20*sin(q[2])))
+m1*g*(x10*cos(q[1])-y10*sin(q[2]));
Q[2] = P*y20-cf*q[2]-m2*g*((x30*cos(q[1])-y30*sin(q[1]))+(x20*cos(q[2])-y20*sin(q[2])));
TKIN = 0.5*(J1+m1*(x10*x10+y10*y10)+
+J2+m2*(x20*x20+y20*y20)*qt[1]*qt[1]+ 0.5*(J2+m2*(x20*x20+y20*y20)*qt[2]*qt[2]+
(J2+m2*(x20*x20+y20*y20)*qt[1]*qt[2]));
EPOT = 0.0;
TU = TKIN - EPOT;
FDIS = 0.0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.