Расчет движения динамической модели наземного буксируемого артиллерийского орудия, страница 2

Рекомендуемые значения характерных физических величин

Вариант 6.2.6

Масса m₁                              1800 кг

Масса m₂                               1900 кг

Момент инерции  J₁             400 кг м²

Момент инерции  J₂             510 кг м²

Координата x₁₀                    3,2 м

Координата y₁₀                    0,5 м

Координата x₂₀                    0,7 м

Координата y₂₀                    0,02 м

Жесткость С_j             2^.10⁶  Н м/рад

Жесткость С_θ             2^.10⁶  Н м/рад

Длина l₁                               3,8 м

Жескость С₁               2^.10⁶  Н м

3.Выбор обобщенных координат

Решение.Система имеет две степени свободы, в качестве обобщенных координат выбираем:

1)  угол поворота   θ  между осью OX₁ и горизонталью (в начальный момент θ₀ = 0 ), ( q₁= θ)

2) угол поворота  j  между осью O₃X₂ и горизонталью (в начальный момент j = j ₀ ), ( q₂=j)

Таким образом, обобщенные координаты:  q₁= θ  , q₂= j , обобщенные скорости: .

4.Расчет кинетической энергии системы

Кинетическую энергию рассматриваемой механической системы представляем  в виде функции времени t, обобщенных координат  q₁ = θ , и обобщенных скоростей

T = T (  .

Кинетическая энергия основания (1) – нижнего станка, массой m1 , совершающего вращение относительно неподвижной оси OZ:

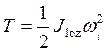 , где                             по теореме Гюйгенса-Штейнера

                                               

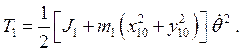
Кинетическая энергия ствола (полого цилиндра) (2) –массой m2 , совершающего вращательное движение вокруг неподвижной оси:

 ,

,               .           

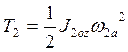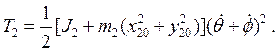
Формулы преобразования координат для центра масс цилиндра имеют следующий вид:   x₂₀=x₂₃ ; y₂₀=y₂₃  ;

              

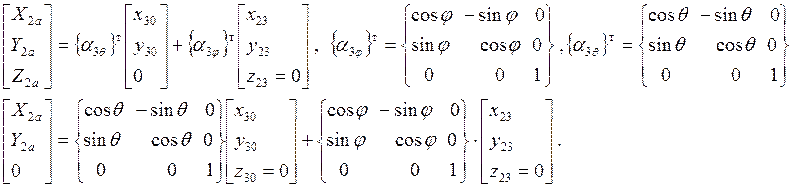
Матрица скоростей:

.

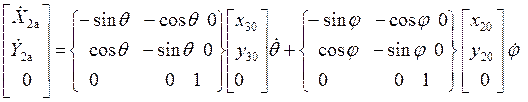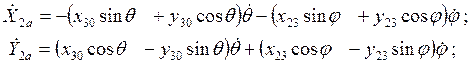
Кинетическая энергия системы:

T = .

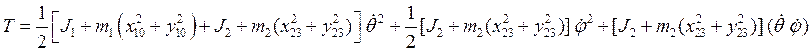
5.Уравнения Лагранжа второго рода для данной системы

1.– для       ;

;

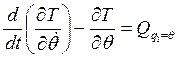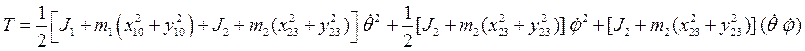
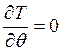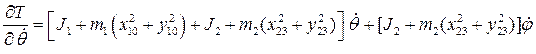
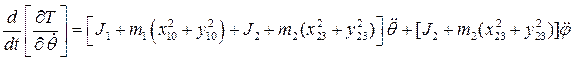
2– для       ;

;

                                                                                                                        

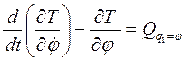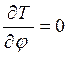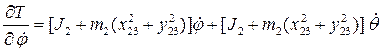
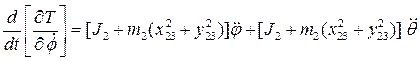
Запишем окончательно левые части уравнений Лагранжа второго рода, оставив только слагаемые со вторыми производными от обобщенных координат. Все остальные слагаемые перенесем в правую часть уравнения, обозначив их как 

1– для     

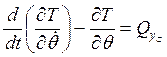
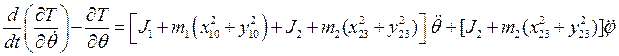
где  

2.– для       ;

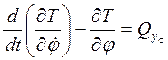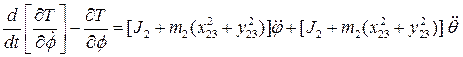
где 

6.Виртуальная работа сил, действующих на рассматриваемую систему.

 Обобщенные силы

Так как обобщённые координаты – независимые друг от друга параметры, то и их вариации тоже независимы. Поэтому, для определения обобщенных сил используем принцип замораживания, находим виртуальные работы, соответствующие виртуальным перемещениям поочередно, от :  

1)  всех заданных активных сил;

2)  сил трения (не заданы) ;

- сил тяжести основания m₁ g       и  ствола   m₂ g 

- силы давления пороховых газов на внутреннюю поверхность дна цилиндра, меняющуюся по следующему закону

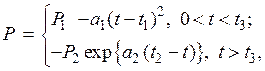                         где постоянные P₁ = 2, 37×10⁶ H;   a₁= 6,68×10¹⁰  H/c² ; t₁ = 0,005 c; P₂ = 0 H;   a₂= 0 H/c²;   t₂= 0 c.

- Момент упругости спиральных пружин жесткостью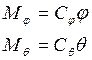

-Сила упругости пружины жесткостью С₁: F_упр= С₁λ=С₁Y_k

                                                                      Y_k= l₁sinθ

                                                                      X_k= l₁cosθ

;   [*]

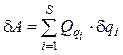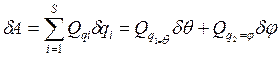1) .

 , где

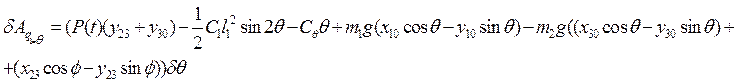
Сравнивая множители в полученном выражении виртуальной работы перед вариацией соответствующей обобщённой координаты и в формуле [*], находим обобщённую силу, соответствующую обобщённой координате q₁₌θ:

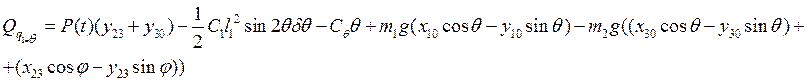
2) .

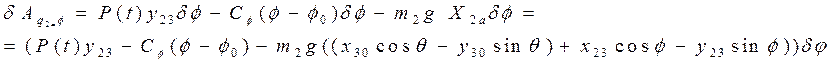
Сравнивая множители в полученном выражении виртуальной работы перед вариацией соответствующей обобщённой координаты и в формуле [*], находим обобщённую силу, соответствующую обобщённой координате q₂ =j

 

Уравнения Лагранжа второго рода в матричной форме

, где   – инерционная матрица, , если  , , если ,

Для   

=

Для   

=

окончательно

1)

2) , где   , если ,    , если , т.е. ;

;

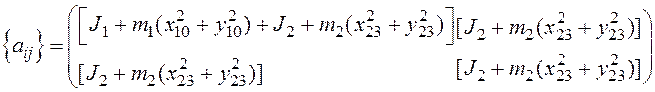
8. ЯЗЫК МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ "MDL"