Введение в метрологию. Измерения и их классификация. Погрешности измерений. Информационно-измерительные системы, страница 9

Пример 1. Число степеней равно 14, и принимаем р = 0.95. Тогда   = 2.62, S_X = 1.583;  и

X= 798.8 ± 4 мм;  P = 0.95.

1.5.3. Обнаружение грубых погрешностей  и их устранение.

Обнаружение грубых погрешностей решается методами проверки статистических гипотез. Проверяемая гипотеза состоит в том, что результат измерения X_k не содержит грубой погрешности. Сомнительным может быть только наибольший  X_max или наименьший    X_min из результатов. Для проверки гипотезы составим величины

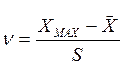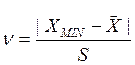 ;  ;                                                1.17

При заданной доверительной вероятности a (обычно, 0.1 или 0.05 ), или уровне значимости  q = 1 - a ,  можно найти те наибольшие значения  n_a , которое случайная величина n может принимать по чисто случайным причинам. Величину n_a можно найти по таблице Приложения 2.

Если выборка достаточно большая (N  > 25), то можно применить простой критерий Романовского выявления промахов, который часто используется на практике. Если для какого-то измеренного значения X_i  выполняется неравенство:

| X_i -  | > 3 S     ,                            (1.18) то это – промах. Этот критерий очень удобен для применения и автоматизации измерений. 

Таким образом, порядок обработки результатов измерений состоит в следующем :

·  определяют точечные оценки истинного значения измеряемой величины и среднеквадратического отклонения результатов измерений,

·  проверяют нормальность распределения результатов измерения (или принятие этой гипотезы без обоснования),

·  задаваясь значениями доверительных вероятностей,  находят доверительные границы результата измерений, и доверительный интервал для среднего квадратического отклонения измерений,

·  определяют наличие грубых погрешностей, и, если последние обнаружены, соответствующие результаты отбрасывают и повторяют вычисления.

1.5.4. Определение погрешностей для косвенных измерений.

Вычисления погрешностей, о которых говорилось выше, относятся к прямым измерениям. Однако наибольшее распространение в настоящее время имеют косвенные измерения. Особенно широко распространены эти измерения в артиллерийских испытаниях. Так, для стендовых испытаний и испытаний вне ствола, важно определить скорость снаряда, или отката ствола, которая вычисляется как отношение расстояния к времени пролета. Практически мы измеряем это расстояние между датчиками (с погрешностью), и время пролета ( с погрешностью). Таким образом, это – типично косвенное измерение.

       Опишем процедуру получения погрешностей для косвенных измерений. Напомним, что при косвенных измерениях значение искомой величины получают на основании известной зависимости, связывающей с другими физическими величинами, которые измеряют прямыми измерениями.

       Рассмотрим общий случай, когда требуется оценить истинное значение величины Z , которая связана с величинами X_m (m=1, . . .,n), которые измеряют прямыми методами. Величина Z связана с X_m (m=1, . . .,n) общим нелинейным соотношением:

Z = F (X₁ , X₂ , . . . , X_n ).                                                                    (1.19)

Найдем оценку матожидания  результата косвенного измерения по результатам матожиданий  прямых измерений, при этом искомая оценка должна иметь наименьшую дисперсию, и следовательно, наибольшую точность среди всех возможных оценок (быть эффективной).

         Считаем, что в процессе измерений величин X_m (m=1, . . .,n) систематические погрешности уже исключены, или пренебрежимо малы по сравнению со случайными погрешностями δ_m (m=1, . . .,n). Также считаем, что измерения величин X_m (m=1, . . .,n) являются независимыми (что обычно выполняется в практике измерений), поэтому сами случайные погрешности δ_m (m=1, . . .,n) тоже независимы друг от друга. Считая, что случайные погрешности малы ( |δ_m | < |X_m |), можно из (1.19) получить следующее разложение:

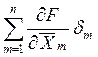Z = F ( ) = F () +  + . . . ;   (1.20)

В (1.20) отброшены члены второго и высших порядков по сравнению с случайными погрешностями. В качестве наиболее достоверной оценки матожидания косвенного измерения получаем из (1.20):