Z = F (![]() )
; (1.21)
)
; (1.21)
Введем частные погрешности косвенного измерения, которые определяют вклад погрешности измерения величины Xm в общую погрешность :
Em = 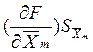 ;
; 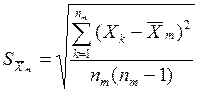 ; (1.22)
; (1.22)
Тогда общую дисперсию косвенного измерения можно оценить формулой:
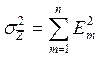 ;
(1.23)
;
(1.23)
Окончательный итог косвенного измерения (для заданной доверительной вероятности Р) записывается в виде:
Z = ![]() ;
(1.24)
;
(1.24)
Здесь число степеней свободы для квантиля Стьюдента tP рассчитывается по формуле:
K = 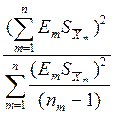 ;
(1.25)
;
(1.25)
Эффективное число степеней свободы К обычно получается дробным, поэтому для отыскания квантиля Стьюдента надо применить интерполяцию.
Существует общепринятый критерий ничтожных погрешностей, с помощью которого можно пренебречь некоторыми погрешностями. Частной погрешностью можно пренебречь, если для нее выполняется неравенство:
Em < ![]() ;
;
ПРИМЕР. Как мы говорили, при
стендовых испытаний важно определить скорость отката ствола. Для этого на
стенде устанавливаются несколько датчиков регистрации положения ствола, причем
датчики устанавливаются на одинаковом расстоянии Н друг от друга. При этом измеряем
разность времени Δt, за которое ствол проходит между двумя соседними
датчиками. Таким образом, можно определить среднюю скорость отката ствола V в промежутке между двумя
датчиками: ![]() . Практически мы измеряем это
расстояние между датчиками с погрешностью δH (обычно
это составляет 1 – 5 мм), и время пролета ( с погрешностью δΔt , которая может
составлять 10-4 – 10-6 с ). Таким образом, это – типично
косвенное измерение, причем типовые значения – это Н ≈ 0.5м, а V0 ≈ 10 м/с , что приводит к типовой оценке для Δt ≈ 5*10-2
c.
. Практически мы измеряем это
расстояние между датчиками с погрешностью δH (обычно
это составляет 1 – 5 мм), и время пролета ( с погрешностью δΔt , которая может
составлять 10-4 – 10-6 с ). Таким образом, это – типично
косвенное измерение, причем типовые значения – это Н ≈ 0.5м, а V0 ≈ 10 м/с , что приводит к типовой оценке для Δt ≈ 5*10-2
c.
В соответствие с (1.20) имеем:
ΔV = δH
/ ![]() +
+ ![]() ) * δΔt =
) * δΔt = ![]() . (1.26)
. (1.26)
В соответствие с нашими
измерениями, имеем ![]() = 0.4 m;
= 0.4 m; ![]() = 0.042 s . Используя данные измерений:
= 0.042 s . Используя данные измерений:
Н = 0.500, 0.501, 0.497, 0.499, 0.503, 0.498, 0.502, 0.500, 0.499, 0.498 м.
Δt = 0.042501, 0.042499, 0.042502, 0.042498, 0.0425, 0.042502, 0.0425, 0.042497, 0.042499, 0.042503 с, необходимо вычислить среднюю скорость и погрешность ее определения по формулам (1.21) – (1.26) .
Приложение 1
Квантили
распределения Стьюдента 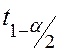
|
Ν |
Уровни значимости, α |
||||||||
|
0,80 |
0,40 |
0,20 |
0,10 |
0,050 |
0,02 |
0,01 |
0,,005 |
0,,001 |
|
|
1 |
0,325 |
1,38 |
3,08 |
6,31 |
12,71 |
31,82 |
63,66 |
127,32 |
636,58 |
|
2 |
0,289 |
1,06 |
1,89 |
2,92 |
4,30 |
6,96 |
9,92 |
14,09 |
31,60 |
|
3 |
0,277 |
0,98 |
1,64 |
2,35 |
3,18 |
4,54 |
5,84 |
7,45 |
12,92 |
|
4 |
0,271 |
0,94 |
1,53 |
2,13 |
2,78 |
3,75 |
4,60 |
5,60 |
8,61 |
|
5 |
0,267 |
0,92 |
1,48 |
2,02 |
2,57 |
3,36 |
4,03 |
4,77 |
6,87 |
|
6 |
0,265 |
0,91 |
1,44 |
1,94 |
2,45 |
3,14 |
3,71 |
4,32 |
5,96 |
|
7 |
0,263 |
0,90 |
1,41 |
1,89 |
2,36 |
3,00 |
3,50 |
4,03 |
5,41 |
|
8 |
0,262 |
0,89 |
1,40 |
1,86 |
2,31 |
2,90 |
3,36 |
3,83 |
5,04 |
|
9 |
0,261 |
0,88 |
1,38 |
1,83 |
2,26 |
2,82 |
3,25 |
3,69 |
4,78 |
|
10 |
0,260 |
0,88 |
1,37 |
1,81 |
2,23 |
2,76 |
3,17 |
3,58 |
4,59 |
|
12 |
0,259 |
0,87 |
1,36 |
1,78 |
2,18 |
2,68 |
3,05 |
3,43 |
4,32 |
|
14 |
0,258 |
0,87 |
1,35 |
1,76 |
2,14 |
2,62 |
2,98 |
3,33 |
4,14 |
|
16 |
0,258 |
0,86 |
1,34 |
1,75 |
2,12 |
2,58 |
2,92 |
3,25 |
4,01 |
|
18 |
0,257 |
0,86 |
1,33 |
1,73 |
2,10 |
2,55 |
2,88 |
3,20 |
3,92 |
|
20 |
0,257 |
0,86 |
1,33 |
1,72 |
2,09 |
2,53 |
2,85 |
3,15 |
3,85 |
|
25 |
0,256 |
0,86 |
1,32 |
1,71 |
2,06 |
2,49 |
2,79 |
3,08 |
3,73 |
|
30 |
0,256 |
0,85 |
1,31 |
1,70 |
2,04 |
2,46 |
2,75 |
3,03 |
3,65 |
|
40 |
0,255 |
0,85 |
1,30 |
1,68 |
2,02 |
2,42 |
2,70 |
2,97 |
3,55 |
|
60 |
0,254 |
0,85 |
1,30 |
1,67 |
2,00 |
2,39 |
2,66 |
2,91 |
3,46 |
|
120 |
0,254 |
0,84 |
1,29 |
1,66 |
1,98 |
2,36 |
2,62 |
2,86 |
3,37 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.