Введение в метрологию. Измерения и их классификация. Погрешности измерений. Информационно-измерительные системы, страница 8

Очевидно, по мере увеличения дисперсии (среднеквадратического отклонения измерения) распределение f(x) расплывается. Это приводит к тому, что вероятность появления больших значений погрешностей возрастает, а вероятность появления меньших погрешностей – уменьшается, т.е., увеличивается рассеивание результатов измерения.

Гауссова функция имеет вид колокола, причем максимум функции достигается в точке  , и сам максимум равен . В практике, вместо s следует применять оценку S.    

 Нормальный закон распределения плотности вероятности соответствует интегральной функции распределения Лапласа вида:

F(x) = P( X < x) =  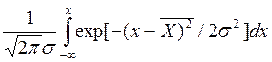                       1.7

Она показывает вероятность того, что случайная величина не превосходит значения х . Ее значения табулированы в таблице (в зависимости от s  и  Р). 

Проверять гипотезу о нормальном распределении результатов  эксплуатационных наблюдений необходимо в ответственных случаях. Проверка может быть проведена несколькими способами. Мы будем применять наиболее простой способ проверки [2].

1.  По результатам эксплуатационных измерений (выборки) вычислим третий m₃ и четвертый m₄ статистический моменты опытного распределения вероятности:

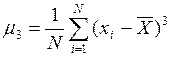 .                                                         1.8

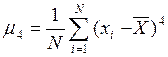      .                                                     1.9

и коэффициенты ассиметрии g₁ и эксцесса g₂ опытного распределения

  ,                          .                        1.10

2.  Определяем средние квадратичные отклонения коэффициентов ассиметрии и эксцесса:

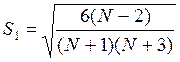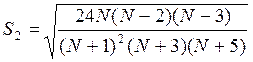  ;        .         1.11

3.  Проводим сравнение полученных величин.

Если выполняются одновременно неравенства:

| g₁ | £ 1.5 S₁   ;        | g₂ + 6 / (N + 1)| £ 1.5 S₂         1.12

то опытные данные подчиняются нормальному распределению.

Если же выполняется хотя бы одно из неравенств:

| g₁ | ³ 3 S₁   ;        | g₂ + 6 / (N + 1)| ³ 2 S₂              1.13

то опытные данные не подчиняются нормальному распределению.

В любом другом случае нельзя дать определенного ответа без дополнительного исследования.

Интервальная оценка математического ожидания измеряемой величины.

Интервальные оценки находятся в виде интервала, который накрывает истинное значение оцениваемой величины с доверительной вероятностью р. Смысл оценки параметра с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенной вероятностью (доверительной) р  находятся истинные значения оцениваемого параметра. Половина доверительного интервала называется доверительной границей d случайного отклонения результатов измерения, соответствующих доверительной вероятности р (для их расчета принимается доверительная вероятность (1+ р) / 2).

Как правило, при обработке результатов измерения решается  задача нахождения интервальной оценки математического ожидания измеряемого параметра при неизвестной дисперсии.

За основу интервальных оценок берутся точечные оценки –  выборочное среднее и выборочная дисперсия измерения:

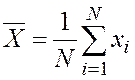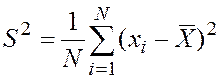  ,                    .                  1.14

Интервальная оценка математического ожидания при

неизвестной дисперсии измерения вычисляется следующим образом. При нормальном распределении генеральной совокупности величина 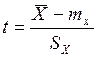 имеет распределение Стьюдента с (N-1) степенями свободы. Таким образом, интервальная оценка математического ожидания запишется в виде:

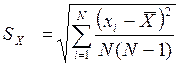.                                      1.15

Здесь величина a - это уровень значимости, который связан с заданной доверительной вероятностью р следующим образом .

Значения квантилей распределения Стьюдента 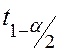 приведены в Приложении 1.

 

Результаты измерений записываются в виде:

X = ;  P = . .  . .   .   ,                                            1.16

Здесь   d =  S_X  t_1-a/2 .

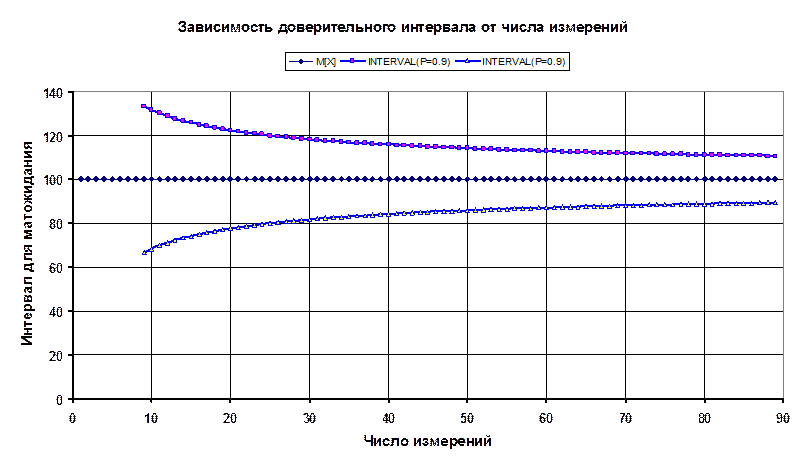
Таким образом, в результате измерения получаем “полосу значений измеряемой величины с несколько расплывчатыми границами”. Истинное значение лежит внутри этих границ, и необязательно, чтобы оно лежало в середине интервала. При этом,  вероятность нахождения результата измерения внутри интервала не стопроцентная, а несколько меньшая (см. рис. Ниже).  Следовательно, нахождение результата измерения вне границ не исключено, хотя и может быть маловероятным.