Введение в метрологию. Измерения и их классификация. Погрешности измерений. Информационно-измерительные системы, страница 7

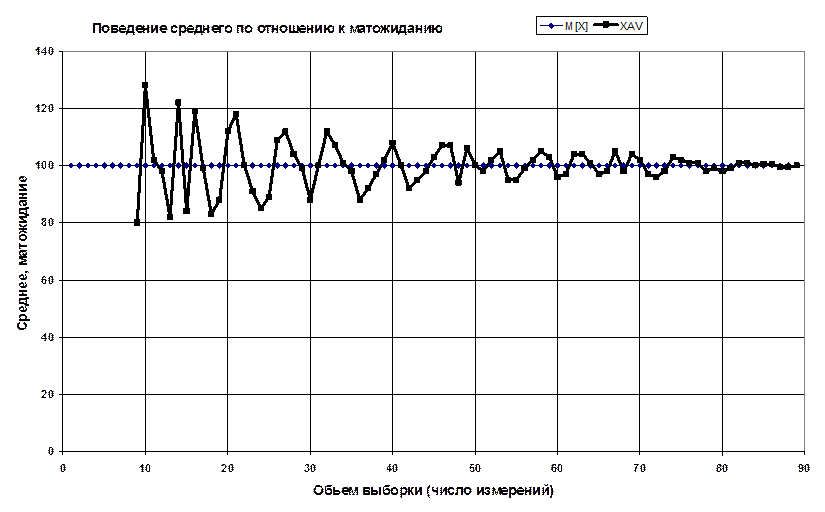
На рис. Ниже показана зависимость среднего арифметического от количества измерений, причем для разного количества измерений  изменяется случайным образом. При этом при увеличении измерений  стремится к матожиданию, что соответствует состоятельности оценки. Вследствие несмещенности оценки для разного числа измерений  располагается как выше, так и ниже истинного матожидания, что приводит к совпадении матожидания от  и истинного математического ожидания результата измерений (напомним, что матожидание многократного измерения – это наиболее вероятное значение результата измеряемой физической величины).

В качестве точечной оценки среднеквадратического отклонения многократного измерения принимается величинаS

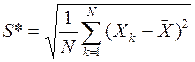 .                                                                        1.3

Среднеквадратическое отклонение измерения,  вычисленное  по этой формуле, является смещенной оценкой, а несмещенной оценкой его является величина S

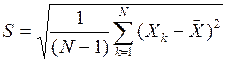.                                                                  1.4

Само среднее значение  тоже является случайной величиной (см. рис.), и его отклонение от истинного значения X  характеризуется дисперсией  S_x для среднего значения, которое вычисляется по формуле

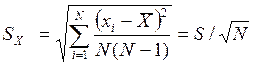.                                                             1.5                           

Как видно из этой формулы, дисперсия среднего значения с ростом N  убывает быстрее, чем s .

Полученные оценки позволяют сделать заключение о точности проведенных измерений. Результаты измерений записываются в виде      X =;  S = . . . ;  S_X =. . . . . ;  N = .  .  .   .

1.5.2 Интервальная оценка результатов измерений

При большом числе испытаний точечные оценки показателей будут приближаться к истинным значениям, но реально большое число испытаний произвести затруднительно. Поэтому в таком случае используют интервальные оценки, достоверность которых характеризуется доверительной вероятностью к результату измерения. Использование интервальных оценок позволяет связать показатели точности и достоверности с числом испытаний.

Для установления такой связи необходимо определить точное распределение выборочной характеристики (статистической оценки) на основе вида закона распределения генеральной совокупности (результата измерения). Поэтому в процессе получения интервальных оценок измерения последовательно решаются четыре задачи:

·  проверка соответствия результатов измерения нормальному закону распределения (или его принятие)

·  вычисление доверительных границ для матожидания результата измерения

·  вычисление доверительных интервалов для среднеквадратического отклонения результата измерения

·  обнаружение грубых погрешностей (промахов).

Нормальный закон распределения вероятности в измерениях.

В процессе эксплуатационных наблюдений на результат измерения параметра Х системы влияет большое число различных по своей природе факторов. Это приводит к вероятностному характеру измеряемой величины. При этом принимают гипотезу о нормальном законе распределения результатов измерений параметра. Широкое распространение нормального распределения погрешностей в практике измерений обьясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которых принимали участие многие математики – Муавр, Лаплас, Гаусс, П.Л. Чебышев, А.М. Ляпунов.

Центральная предельная теорема говорит о том, что распределение случайных погрешностей будет близко к нормальному закону, когда результаты измерения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. Именно поэтому, в измерениях, обычно принимают гипотезу о нормальном распределении погрешностей измерения.

То-есть, измеряемый параметр X  имеет нормальное распределение cо средним (математическим ожиданием)  и дисперсией σ²:

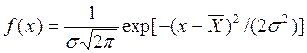.                               1.6