Министерство высшего и среднего специального образования Балтийский государственный технический университет «Военмех» им. Д.Ф. Устинова
Кафедра электротехники
Расчёт переходных процессов
Студент: Ефремов А.Ю.
Группа: Н231
Преподаватель: Погромская Л.Ф.
Санкт-Петербург 2005
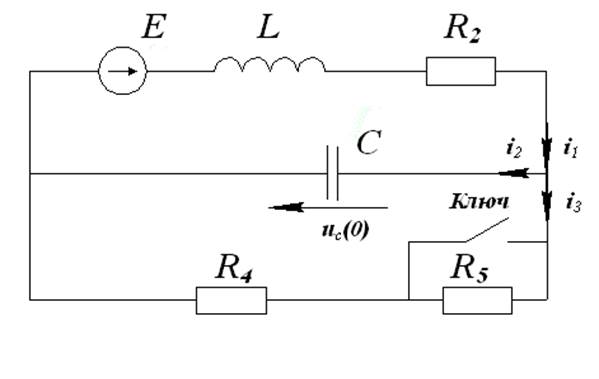
Схема 1
E=100 B, R2=R4=300 Ом, R5=600 Ом, C=5 мкФ, L=0,09 мГн
При t=0 ключ размыкается
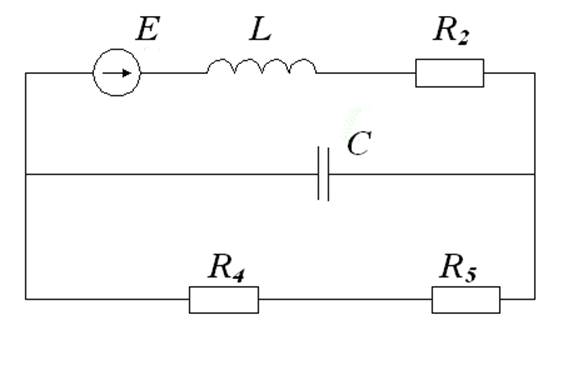
Схема 2
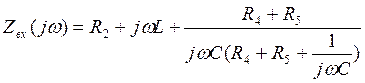 (1.1.)
(1.1.)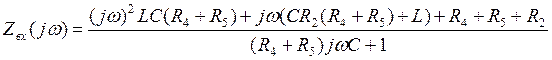 (1.2.)
(1.2.)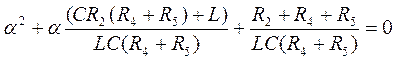 (1.4.)
(1.4.)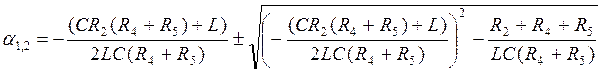 (1.5.)
(1.5.)
Подставим числовые значения:
Корни характеристического уравнения:
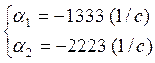 (1.6.)
(1.6.)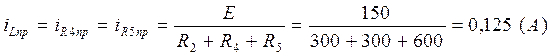
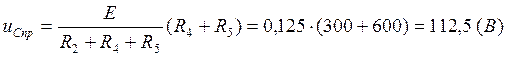 (2.3.)
(2.3.) ![]() (2.4.)
(2.4.)
![]() (2.5.)
(2.5.)
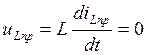 (2.7.)
(2.7.)Рассмотрим схему 1 до коммутации. Так как i1 =iL получаем:
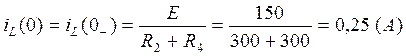
(3.1.)
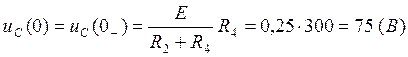 (3.2.)
(3.2.)
б) Определение зависимых начальных условий
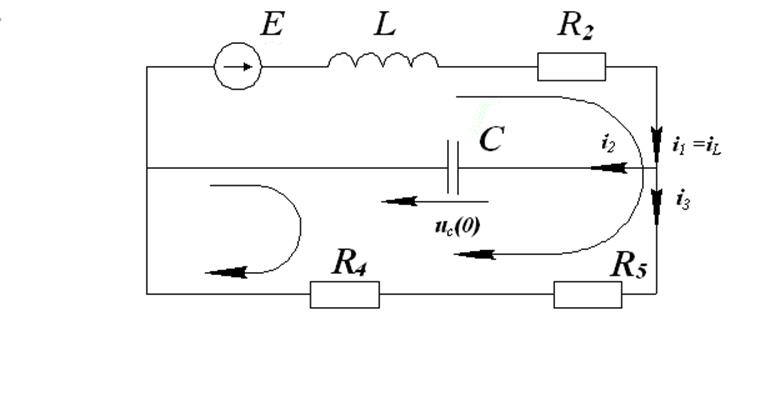
Схема 3
Зависимые начальные условия определим из системы, составленной по законам Кирхгофа:
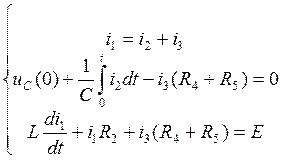 (3.3.)
(3.3.)
При t=0 имеем: 
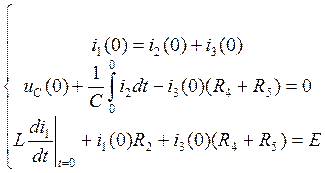 (3.4.)
(3.4.)
Из второго уравнения системы (3.4):
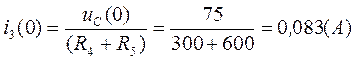
(3.5.)
Из первого уравнения системы (3.4):
![]() (3.6.)
(3.6.)
Из третьего уравнения системы (3.4):
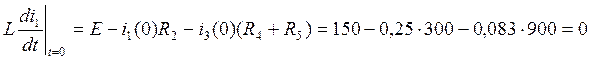 (3.7.)
(3.7.)
![]() (3.8.)
(3.8.)
![]() (3.9.)
(3.9.)
![]() (3.10.)
(3.10.)
4.
Составление дифференциального уравнения по законам Кирхгофа
Воспользуемся составленной ранее системой (3.3). Из третьего уравнения системы (3.3):
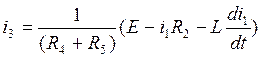 (4.1.)
(4.1.)
Дифференциируем второе уравнение системы (3.3) по t:
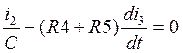 (4.2.)
(4.2.)
 (4.3.)
(4.3.)
Дифференциируем (4.1) по t:
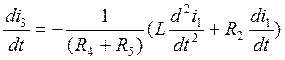 (4.4.)
(4.4.)
Подставляем (4.4) в (4.3):
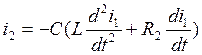 (4.5.)
(4.5.)
Подставляем (4.1) и (4.5) в первое уравнение системы (3.3):
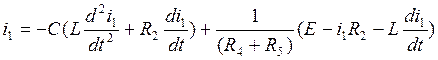 (4.6.)
(4.6.)
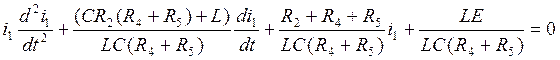 (4.7.)
(4.7.)
Отметим, что в уравнении (4.7) все знаки перед искомым током и его производными одинаковы. Сравним коэффициенты перед искомым током и его производными с характеристическим уравнением (уравнение (1.4)). Коэффициенты совпадают.
5. Составление дифференциального уравнения методом Д-алгебраизации
Применим метод Д-алгебраизации для системы (3.3), составленной по законам Кирхгофа. При этом 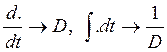
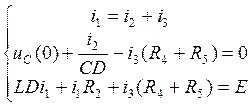 (5.1.)
(5.1.)
Решаем полученную систему алгебраических уравнений. Для этого выражаем из первого уравнения системы (5.1) ток i2:
![]() (5.2.)
(5.2.)
Затем подставляем (5.2) во второе уравнение системы (5.1):
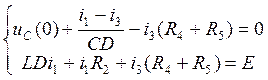 (5.3.)
(5.3.)
Приведём уравнение (5.3) к виду, необходимому для решения методом Крамера:
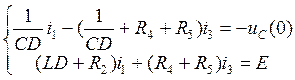 (5.4.)
(5.4.)
Решаем систему (5.4) методом Крамера:
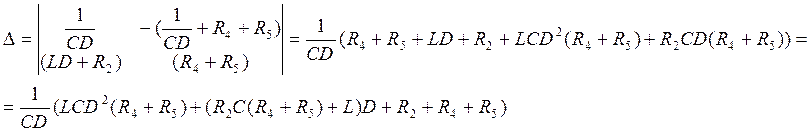
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.