Расчет переходных процессов (E=100 В, L=0,09 мГн, R2=300 Ом, R5=600 Ом, C=5 мкФ, ключ размыкается), страница 2

Коэффициенты этого полинома совпадают с коэффициентами характеристического.

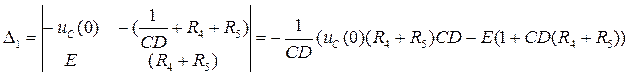
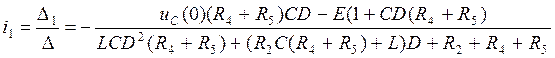                         (5.5.)

Домножаем уравнение (5.5) на знаменатель правой части 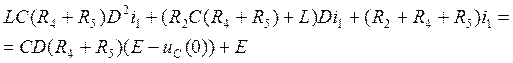                                                                (5.6.)                                                                          

В уравнении (5.1) делаем замену, обратную приведённой выше:

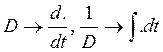
При этом =0

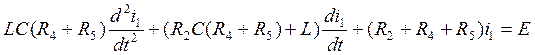                                  (5.7.)

Разделим  уравнение (5.7) на :

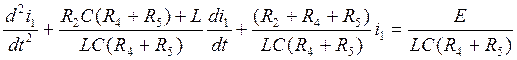                                      (5.8.)

6. Анализ полученного дифференциального уравнения а.) Проверка размерности коэффициентов a,b.

Коэффициенты a и b должны иметь следующую размерность:

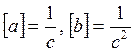                                                                                                                  (6.1.)

В нашем случае:

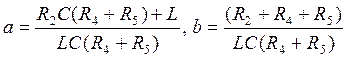                                                                        (6.2.)

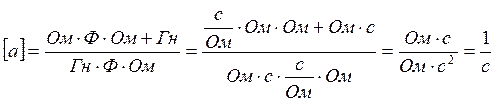                                          (6.3.)

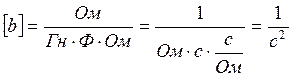                                                                                  (6.4.)

Коэффициенты a и b имеют необходимые размерности.

б.) Проверка правой части.

Найдём принуждённую составляющую тока i₁ из уравнения (5.8). Производные от постоянной величины равны нулю, поэтому выражаем искомую величину:

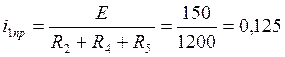                                                                                    (6.5.)

Значение принуждённой составляющей совпадает со значением, найденным в пункте 2 (уравнение 2.2).

7.Решение полученного  дифференциального уравнения классическим методом

Так как корни в пункте 1 получились вещественными (формула 1.6), ищем ток в виде суммы принуждённой и свободной составляющих. Из пункта 2 (А).

                                                                                                           (7.1.)

                                                                                                    (7.2.)

Подставим слева начальные условия, а справа момент времени t=0:

                                                                        (7.3.)

Продифференциируем уравнение (7.2) по t:

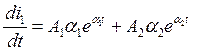                                                                                                     (7.4.)

Подставим  в уравнения (7.3) и (7.4) слева начальные условия, а справа - момент времени t=0:

                                                                                                                   (7.5.)

Получили систему уравнений:

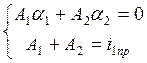                                                                                                                (7.6.)

Решим систему уравнений (7.6) методом Крамера:

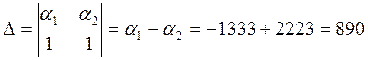
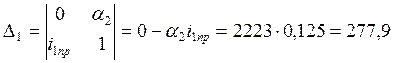
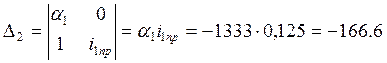
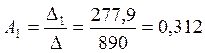
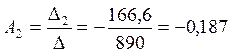
Запишем искомый ток с учётом найденных постоянных интегрирования:

                                                                                (7.7.)

8. Определение остальных токов и напряжений

Воспользуемся законами Кирхгофа и уравнениями связи (Схема 3)

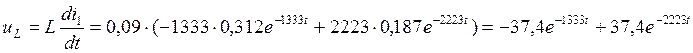  (8.1.)

      (8.2.)

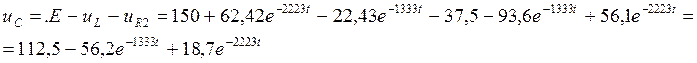  (8.3.)

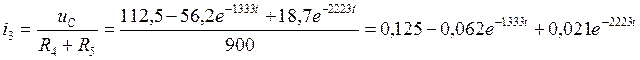             (8.4.)

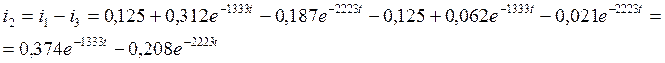        (8.5.)

        (8.6.)

        (8.7.)

9. Таблица проверок

Ве-ли-чина	Уравнение	t<0	t=0
			По з.К.	Рас-чёт	По з.К.	Рас-чёт
i1(A)				0,25	=0,125	0,125
i2(A)				0,166		0
i3(A)				0,084	=0,125	0,125
uR2			=75	75		37,5
uR4			=25	25,2		37,5
uR5		0	=50	50,4		75
uL				0		0
uC				75		112,5

10. Решение полученного  дифференциального уравнения операторным методом