Балтийский Государственный
Технический Университет
«ВоенМех»
имени Д.Ф. Устинова
Домашняя работа
по теоретическим основам электротехники
на тему:
Расчет нелинейных цепей
Вариант 14
Выполнил: Суханов А.В.
Группа: И433
Проверил: Чередниченко Л.А.
Санкт-Петербург 2005
Домашняя работа по ТОЭ
Тема: Расчет нелинейных цепей.
Задание: Катушка
с ферромагнитным сердечником, имеющая 200 витков , включена в цепь, питаемую
источником постоянного напряжения 7,5. Параметры схемы: R1=4 Ом, R2=5 Ом, Сопротивление катушки 2 Ома.
Вольт-амперная характеристика нелинейного резистора апроксимируется выражением ![]() . Требуется:
. Требуется:
1. Найти магнитные потоки в ветвях ферромагнитного сердечника методом графического суммирования вебер-амперных характеристик.
2. Проверить полученные результаты путем решения обратной задачи.
3. Найти статическую индуктивность катушки при заданном токе.
Схема:
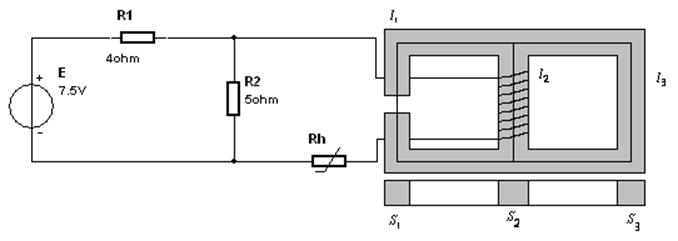
Параметры цепи:
![]() В - источник постоянного напряжения
В - источник постоянного напряжения
![]() Ом
Ом
![]() Ом
Ом
![]() Ом - сопротивление
провода катушки
Ом - сопротивление
провода катушки
![]() -
вольт-амперная характеристика нелинейного резистора Rh
-
вольт-амперная характеристика нелинейного резистора Rh
Параметры ферромагнитного сердечника:
![]() см2 -
площадь поперечного сечения первой ветви
см2 -
площадь поперечного сечения первой ветви
![]() см2 -
площадь поперечного сечения второй ветви
см2 -
площадь поперечного сечения второй ветви
![]() см2 -
площадь поперечного сечения третьей ветви
см2 -
площадь поперечного сечения третьей ветви
![]() см - длина
первой ветви
см - длина
первой ветви
![]() см - длина второй
ветви
см - длина второй
ветви
![]() см - длина
третьей ветви
см - длина
третьей ветви
![]() мм – длина зазора в первой ветви
мм – длина зазора в первой ветви
Кривая намагничевания материала сердечника:
|
H |
А/м |
0 |
10 |
20 |
40 |
60 |
80 |
120 |
200 |
400 |
600 |
800 |
1000 |
|
B |
Тл |
0 |
0.08 |
0.22 |
0.75 |
0.93 |
1.02 |
1.14 |
1.38 |
1.47 |
1.53 |
1.57 |
1.61 |
Решение задачи
1. Нахождение тока, протекающего через обмотку катушки.
Ток рассчитывается методом эквивалентного генератора. Линейная часть цепи представляется эквивалентным источников ЭДС. Находится ток, текущий через нелинейный элемент. Так как катушка соединена последовательно с нелинейным резистором, то через катушку будет протекать такой же ток.
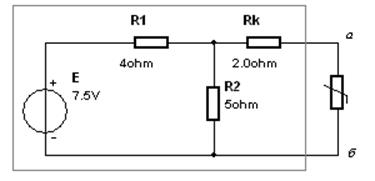
Рис.1 Выделение эквивалентного генератора.
a. Нахождение ЭДС генератора.
ЭДС генератора рассчитывается как напряжение на зажимах “а” и “б” при отключенном сопротивлении Rн.
Преобразуем соединение звездой в соединение треугольником:
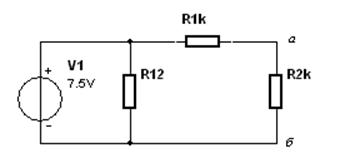
Рис.2 Преобразование соединения в треугольник.
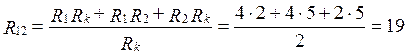 Ом
Ом
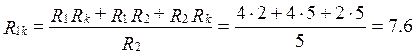 Ом
Ом
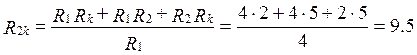 Ом
Ом
После преобразования видно, что 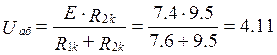 В
В
![]() В
В
b. Нахождение внутреннего сопротивления генератора.
Внутреннее сопротивление этого источника находится как сопротивление всей прочей цепи (Рисунок 1) между зажимами “а” и “б” при замкнутом накоротко источнике ЭДС.
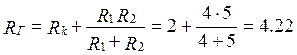 Ом
Ом
c. Уравнение по II закону Киргофа для схемы с эквивалентным генератором.
![]()
![]()
Решеним этого уравнения будет ![]() А. То есть, ток, протекающий через
нелинейный резистор и, соответственно, через катушку будет равен 0.46 А
А. То есть, ток, протекающий через
нелинейный резистор и, соответственно, через катушку будет равен 0.46 А
2. Расчет магнитной цепи при известной магнитодвижущей силе.
Определяем магнитное сопротивление воздушного зазора:
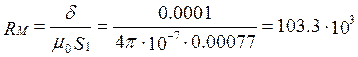 Гн-1
Гн-1
Строим на графике вебер-амперную
характеристику воздушного зазора 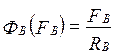
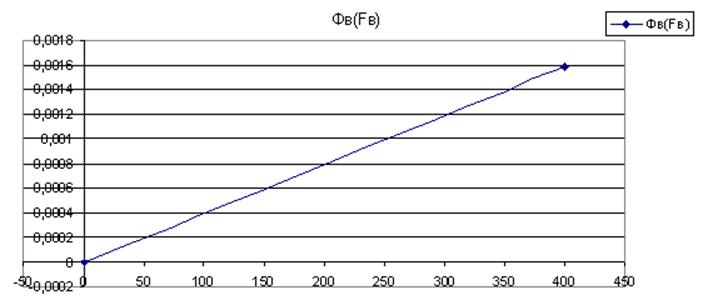
Вебер-амперную характеристику
стального участка первой ветви строим по кривой намагничевания, учитывая, что ![]() и
и ![]()
|
F1 |
0 |
1,95 |
3,9 |
7,8 |
11,7 |
15,6 |
23,4 |
|
Ф1 |
0 |
0,0000616 |
0,000169 |
0,000578 |
0,000716 |
0,000785 |
0,000878 |
|
F1 |
39 |
78 |
117 |
156 |
195 |
||
|
Ф1 |
0,000986 |
0,001132 |
0,001178 |
0,001209 |
0,00124 |
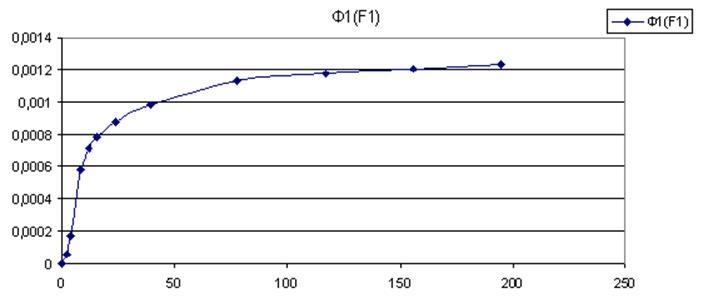
Магнитодвижущая сила первой ветви
![]() . Так как
. Так как ![]() , то,
складывая абциссы кривых
, то,
складывая абциссы кривых ![]() и
и ![]() , получим вебер-амперную характеристику
первой ветви
, получим вебер-амперную характеристику
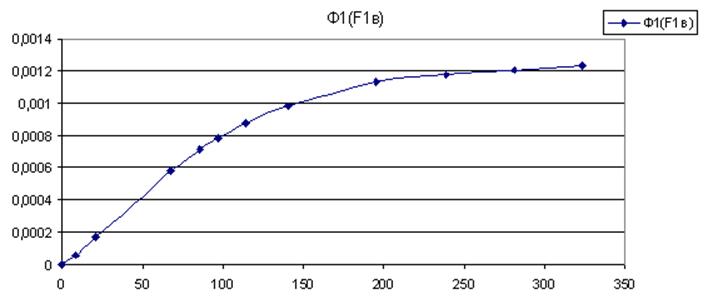
первой ветви ![]() :
:
|
F1В |
0 |
8,31328 |
21,39902 |
67,45575 |
85,67313 |
96,73182 |
114,0767 |
|
Ф1 |
0 |
0,0000616 |
0,000169 |
0,000578 |
0,000716 |
0,000785 |
0,000878 |
|
F1В |
140,8125 |
194,9253 |
238,6977 |
280,8794 |
323,061 |
||
|
Ф1 |
0,000986 |
0,001132 |
0,001178 |
0,001209 |
0,00124 |
Магнитодвижущая сила ![]() является общей для первой и третьей ветви.
Строим вебер-амперную характеристику третьей ветви
является общей для первой и третьей ветви.
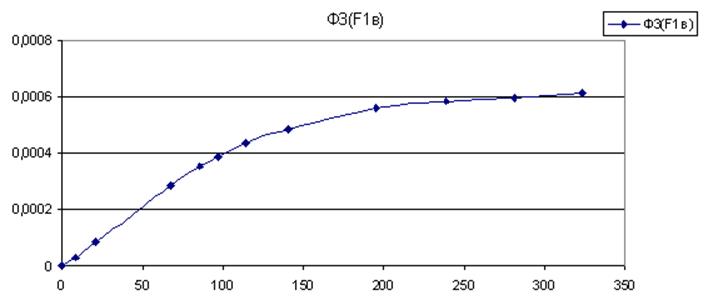
Строим вебер-амперную характеристику третьей ветви ![]() ,
учитывая, что
,
учитывая, что ![]()
|
F1В |
0 |
8,31328 |
21,39902 |
67,45575 |
85,67313 |
96,73182 |
114,0767 |
|
Ф3 |
0 |
0,0000304 |
8,36E-05 |
0,000285 |
0,000353 |
0,000388 |
0,000433 |
|
F1В |
140,8125 |
194,9253 |
238,6977 |
280,8794 |
323,061 |
||
|
Ф3 |
0,000486 |
0,000559 |
0,000581 |
0,000597 |
0,000612 |
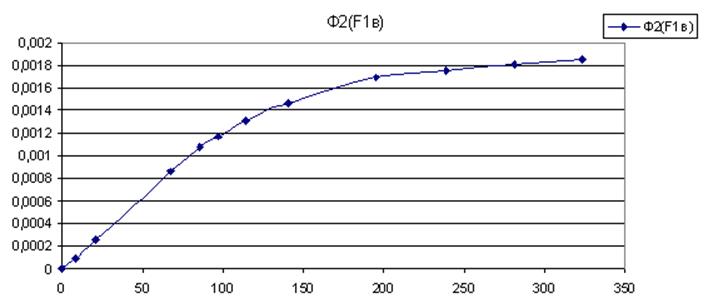
Используя соотношение ![]() , складываем ординаты кривых
, складываем ординаты кривых ![]() и
и ![]() и
получаем кривую
и
получаем кривую ![]()
|
F1В |
0 |
8,31328 |
21,39902 |
67,45575 |
85,67313 |
96,73182 |
114,0767 |
|
Ф2 |
0 |
0,000092 |
0,000253 |
0,000863 |
0,00107 |
0,001173 |
0,001311 |
|
F1В |
140,8125 |
194,9253 |
238,6977 |
280,8794 |
323,061 |
||
|
Ф2 |
0,001472 |
0,001691 |
0,00176 |
0,001806 |
0,001852 |
Для второй ветви строим
зависимость ![]() , учитывая, что
, учитывая, что ![]() и
и ![]()
|
Iw-F2 |
92 |
91 |
90 |
88 |
86 |
84 |
80 |
|
Ф2 |
0 |
0,0000168 |
4,62E-05 |
0,000158 |
0,000195 |
0,000214 |
0,000239 |
|
Iw-F2 |
72 |
52 |
32 |
12 |
-8 |
||
|
Ф2 |
0,000269 |
0,000309 |
0,000321 |
0,00033 |
0,000338 |
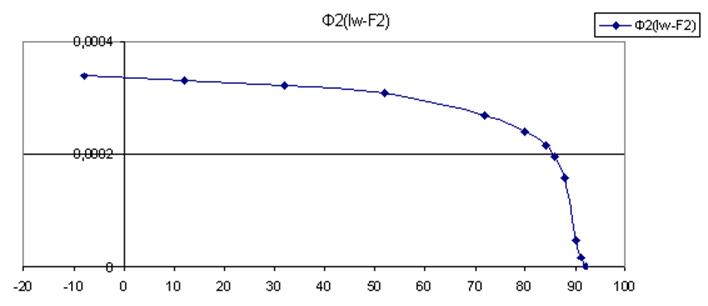
При совмещении графиков получаем:
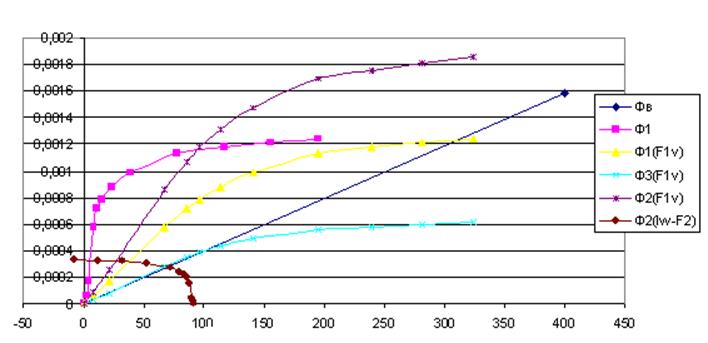
Находим точку пересечения кривых ![]() и
и ![]() ,
которая дает искомое значение магнитного потока
,
которая дает искомое значение магнитного потока ![]() во
второй ветви:
во
второй ветви:
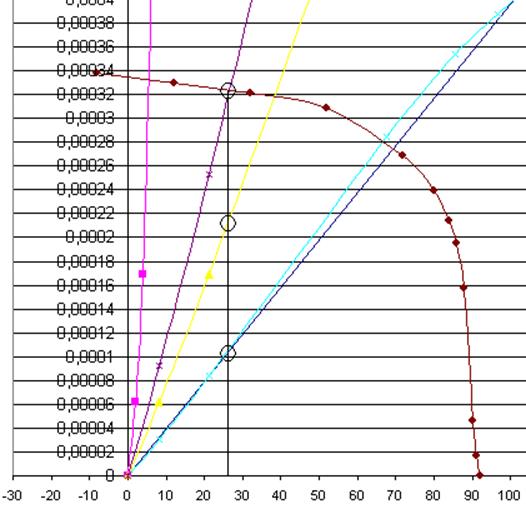
Из рисунка видно:
![]() мВб
мВб
![]() мВб
мВб
![]() мВб
мВб
3. Расчет магнитной цепи при известном магнитном потоке.
Для проверки правильности
полученных результатов решаем обратную задачу – считаем заданным один из
найденных магнитных потоков и находим соответсвующую ему магнитодвижущую силу ![]() . Целесообразно задаться найденным
значением
. Целесообразно задаться найденным
значением ![]() мВб.
мВб.
Находим ![]() А,
затем определяем индукцию в стальном участке первой ветви
А,
затем определяем индукцию в стальном участке первой ветви 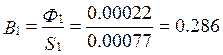 Тл. По кривой намагничевания находим
значение
Тл. По кривой намагничевания находим
значение ![]() , соответсвующее
, соответсвующее ![]() :
:
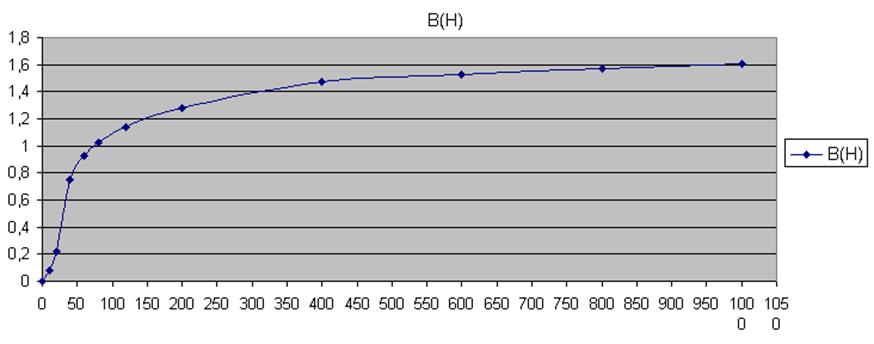
![]() А/м.
Определяем
А/м.
Определяем ![]() А
А
Далее вычисляем ![]() А,
А, 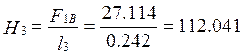 А/м.
По кривой
А/м.
По кривой ![]() определяем
определяем ![]() Тл и
далее
Тл и
далее ![]() Вб. Поток во второй ветви
Вб. Поток во второй ветви ![]() Вб.
Вб. 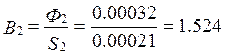 Тл. По
кривой
Тл. По
кривой ![]() определяем
определяем ![]() А/м, и
затем
А/м, и
затем ![]() А. Наконец, определяем магнитодвижущую силу
обмотки
А. Наконец, определяем магнитодвижущую силу
обмотки ![]() А
А
4. Статическая индуктивность катушки.
Статическая индуктивность
определяется по формуле 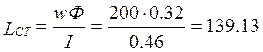 Гн
Гн
Где Ф – значение магнитоного потока в ветви, на которой размещена обмотка. I – ток в обмотке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.