Министерсво Образования Российской Федерации
Балтийский Государственный Университет им. Д.Ф.Устинова
“ВоенМех”
Кафедра электротехники.
Курсовая работа по
теоретическим основам электротехники.
“Расчет переходного процесса.”
вариант №22
Студент: Мазинская Е.А.
Группа: И-311
Проверил: проф. Галайдин П.А.
Санкт-Петербург
2003 г.
Содержание:
1.Электрическая схема рассчитываемой цепи……………………………3
2.Расчет принужденного режима………………………………………….4
3.Составление дифференциальных уравнений…………………………...5
4.Определение начальных условий……………………………………….7
5.Решение дифференциального уравнения……………………………….9
6.Определение остальных токов и напряжений………………………….11
7.Решение дифференциального уравнения операторным способом…...12
8.Сравнение результатов…………………………………………………..15
9.Графики токов и напряжений…………………………………………...15
10.Заключение……………………………………………………………...17
11.Список литературы……………………………………………………..18
В цепи, изображенной на рис. 1, происходит коммутация в момент времени t = 0 (ключ размыкается).
Е = 100 В
L = 0.2 Гн
C = 7 мкФ
R1 = 400 Ом
R2 = 200 Ом
R3 = 600 Ом
![]()
![]() (1)
(1)
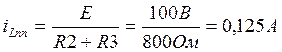 (2)
(2)
![]()
![]()
![]()
![]() (3)
(3)
По II закону Кирхгофа:
![]() (4)
(4)
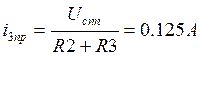 (5)
(5)
![]()
![]()
![]()
Исходная система уравнений для момента времени после коммутации содержит 2 уравнения, записанные по законам Кирхгофа, и одно уравнение связи:
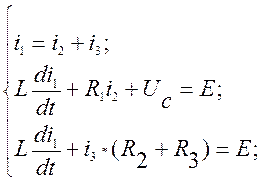
(6)
Из первого уравнения системы (6) выразим:
![]()
![]() (7)
(7)
Из второго уравнения выразим ![]() :
:
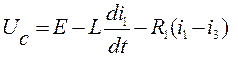 (8)
(8)
Из третьего уравнения выразим ![]() :
:
![]() = (
= (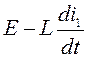 )*
)*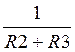
![]()
![]() (9)
(9)
![]() =
= ![]() -
- 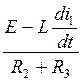 (10)
(10)
Используя уравнение связи 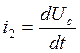 и значение
и значение ![]() из
формулы (8), получим:
из
формулы (8), получим:
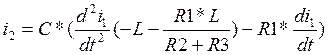 (11)
(11)
Подставляя в формулу (7) выражения для ![]()
![]() и
и
![]() из формул (9), (10) соответственно,
получим:
из формул (9), (10) соответственно,
получим:
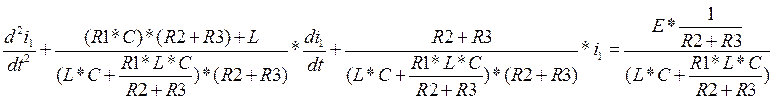
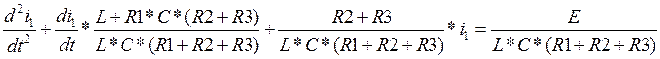 (12)
(12)
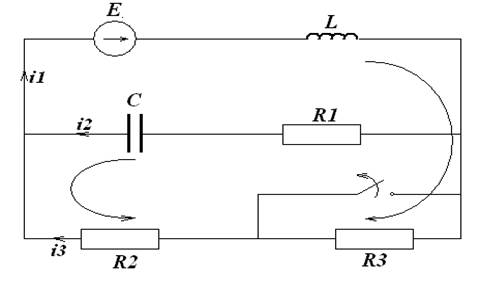
Проверка ilпр:
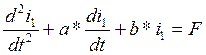
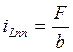
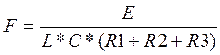
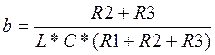
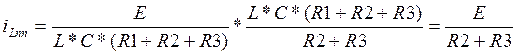 (13)
(13)
Проверка размерностей a и b:
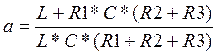
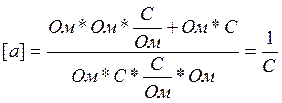
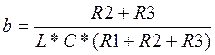
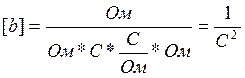
4.Определение начальных условий.
а) независимые
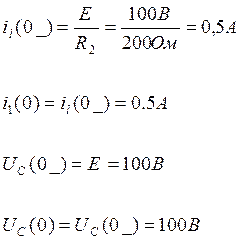
б) зависимые
Составим систему уравнений по ЗК:
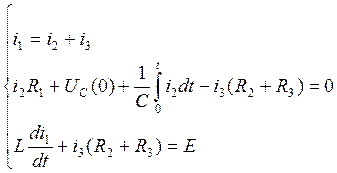 (14)
(14)
Система уравнений в момент времени t=0:
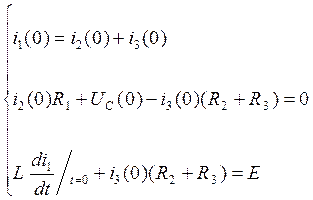 (15)
(15)
Из первого уравнения системы
(15) выразим ![]() и подставим его во второе
уравнение, получим:
и подставим его во второе
уравнение, получим:
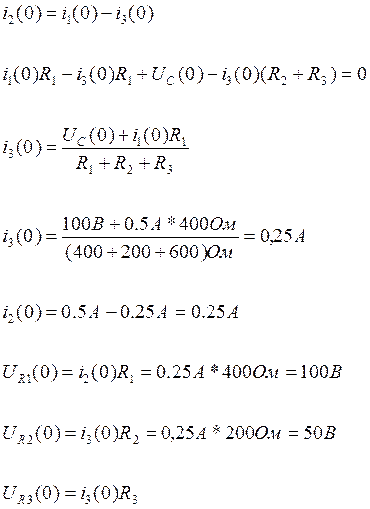
(16)
(17)
Из третьего уравнения системы (15) выразим 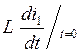
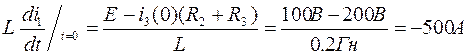
(18)
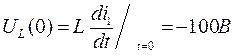 (19)
(19)
5.Решение дифференциального уравнения.
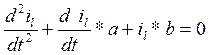
(20)
![]()
Составим характеристическое уравнение по Zвх:
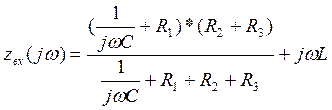 (21)
(21)
Пусть ![]() ,
,
![]()
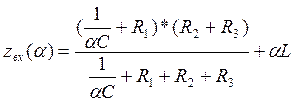 (22)
(22)
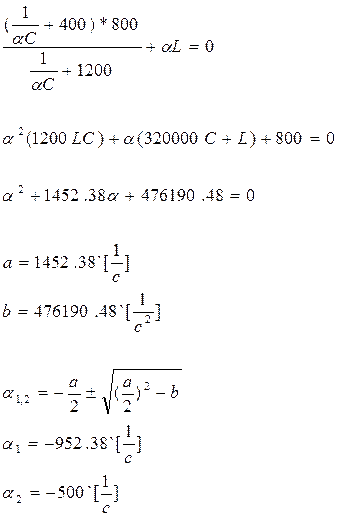
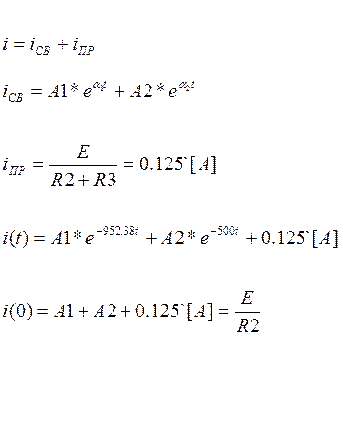 Из
начальных условий:
Из
начальных условий:
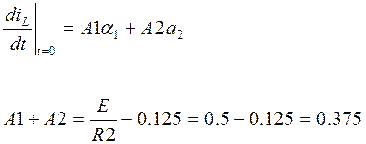 (23)
(23)
(24)
Подставляя значение для  из
формулы (18) в формулу (23) получим
из
формулы (18) в формулу (23) получим
![]() (25), где
(25), где 
Совместно решая уравнения (24), (25) получим:
A1 = 0,691 [A]
A2 = -0,316 [A]
![]() [A] (26)
[A] (26)
6.Определение остальных токов и напряжений:
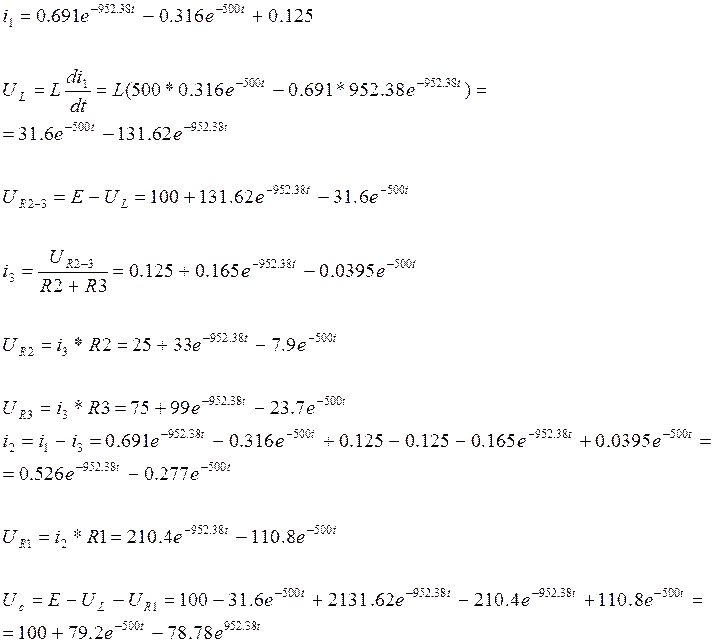 [A]
[A]
![]()
[B]
[B]
[A]
[B]
[B]
[A]
[B]
[B]
7. Решение дифференциального уравнения операторным способом:
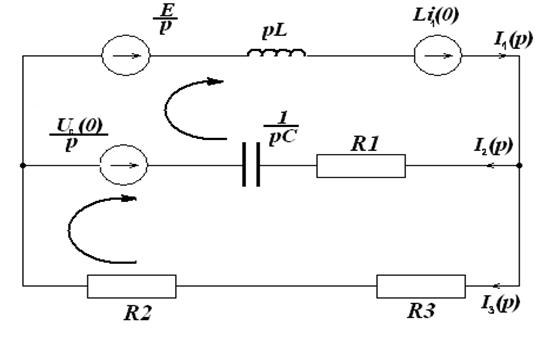
Рис.2 Операторная схема замещения.
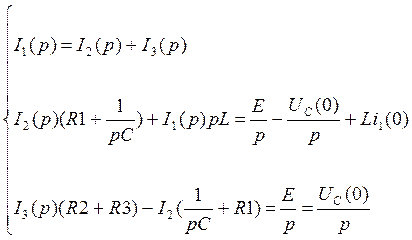 (27)
(27)
Сложим второе и третье уравнения системы (27):
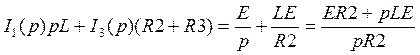
Из первого уравнения системы (27) ![]() ,
подставим полученное выражение для
,
подставим полученное выражение для ![]() в третье уравнение
системы (27)
в третье уравнение
системы (27)
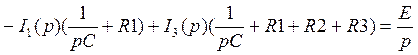
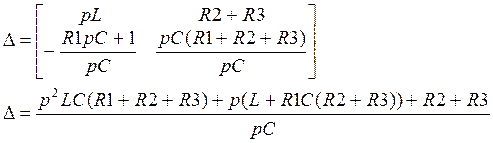
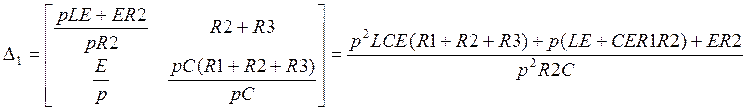
![]() =
=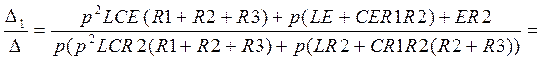
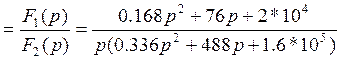
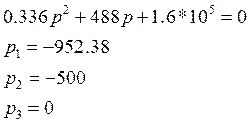
Перейдем от изображения к оригиналу с помощью теоремы разложения:
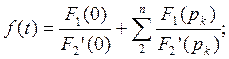
(28)
![]()
![]()
![]()
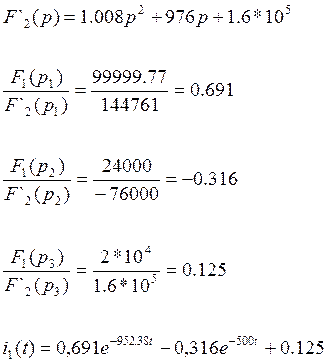
8.Сравнение результатов.
Ток![]() , найденный классическим методом,
совпадает с током, найденным операторным методом
, найденный классическим методом,
совпадает с током, найденным операторным методом ![]()
9.Графики токов и напряжений:
Графики изменения токов i1(t), i2(t) и i3(t) приведены на рис. 3.
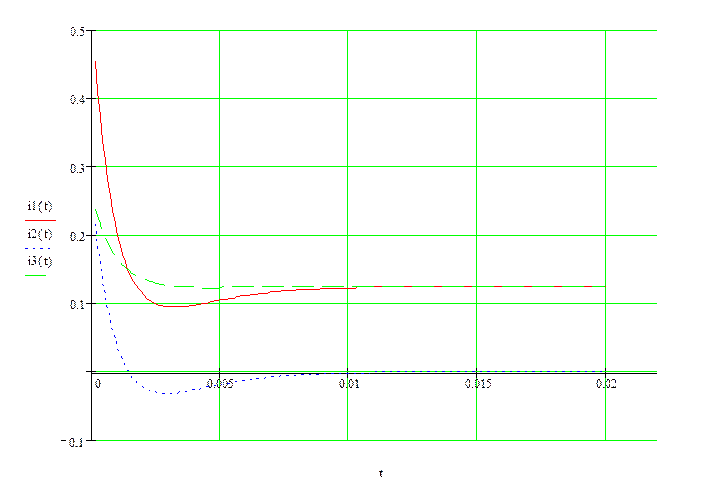
Рис.3
Проверка токов по 1 Закону Кирхгофа:
i1(0.001) – i2(0.001) – i3(0.001) = 0,2-0,035-0,165 = 0,
i1(0.003) – i2(0.003) – i3(0.003) = 0.094-(-0,032)-0,126 = 0.
Графики изменения напряжений ![]() приведены
на рис. 4.
приведены
на рис. 4.
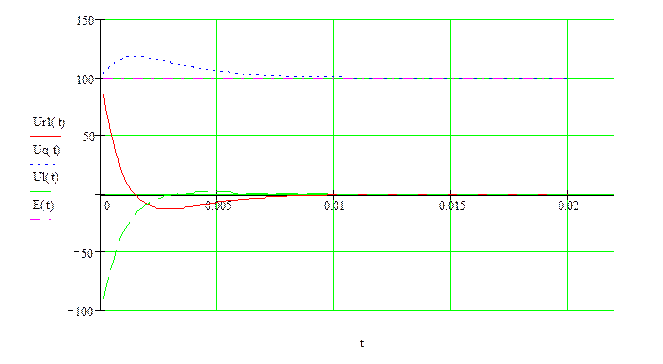
Рис.4
Проверка напряжений по 2 Закону Кирхгофа:
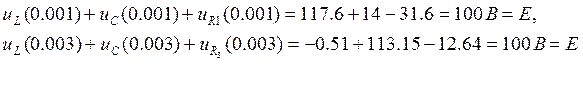
10.Заключение:
В ходе выполнения работы расчеты производились 2 методами (классическим и операторным), которые дали одинаковые результаты:
![]()
![]()
![]()
![]()
![]()
![]()
Список литературы:
3. Л.А.Бессонов. Теоретические основы электротехники. Москва, 2001.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.